深蓝学院运动规划L8

模型预测控制在运动规划中的应用

Introduction

线性MPC解决的优化问题一般是凸的

非线性MPC解决的优化问题一般是非凸的

• 模型

  • 系统模型（描述系统自身）
  • 问题模型（描述优化目标）

• 预测

  • 状态空间

  • 输入空间

  • 参数空间

    💡 示例

    实际的输入F是连续，这会使得优化问题的维度是无限维，因此可以进行一些操作，把输入空间转化为参数空间，比如把力的优化看做多项式，进而将求最优的F转为求最优多项式参数。

• 控制（选择最优的输入或策略）

$x\notin Obstacle$也相当于不等式约束，但由于该约束一般为非凸的，因此需要特殊处理

零阶保持器（离散）、多项式、B样条

数值映射的方法：Jerk limited trajectory、基于神经网络的方法

优化的方法：

• Searching
• Convex optimization
• Noconvex optimization
  • 顺序二次规划
  • 粒子群优化（适用于非凸、非线性、离散的情况）

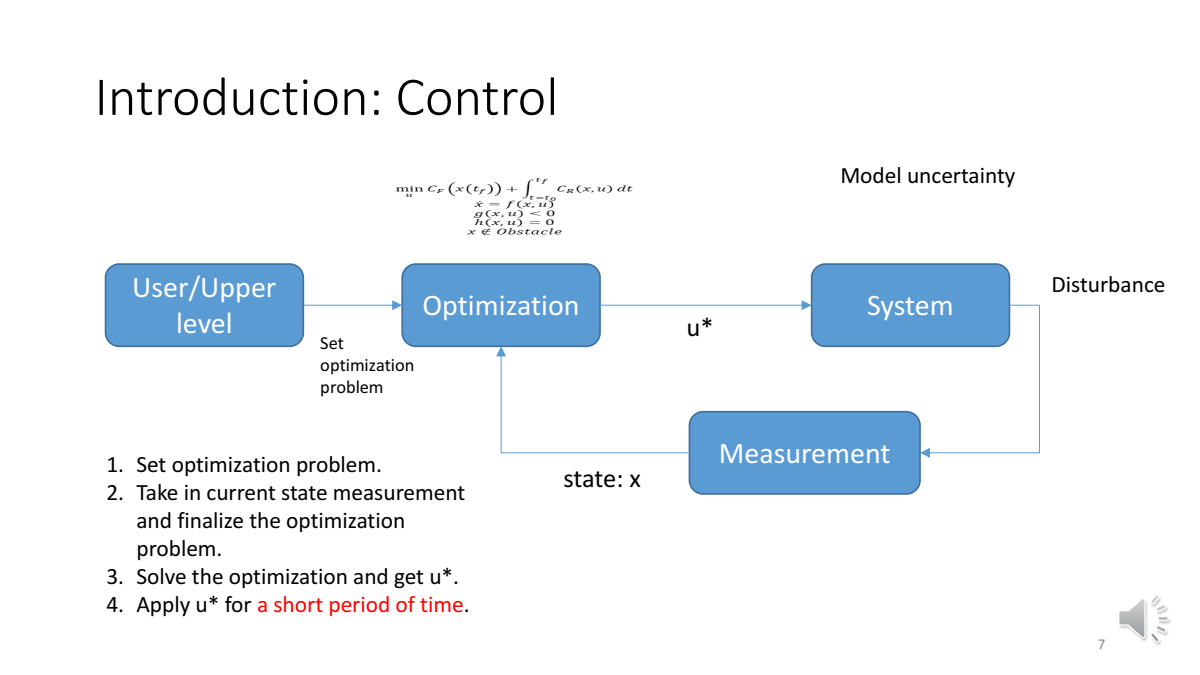
RHC（Receding Horizon Control），MPC的基础。

• 建立优化问题
• 获取当前的状态（作为优化问题的初始状态），确定优化问题
• 求解优化问题，得到$u^*$
• 将$u^*$直接用于短时间的状态控制
• 循环2—4步……

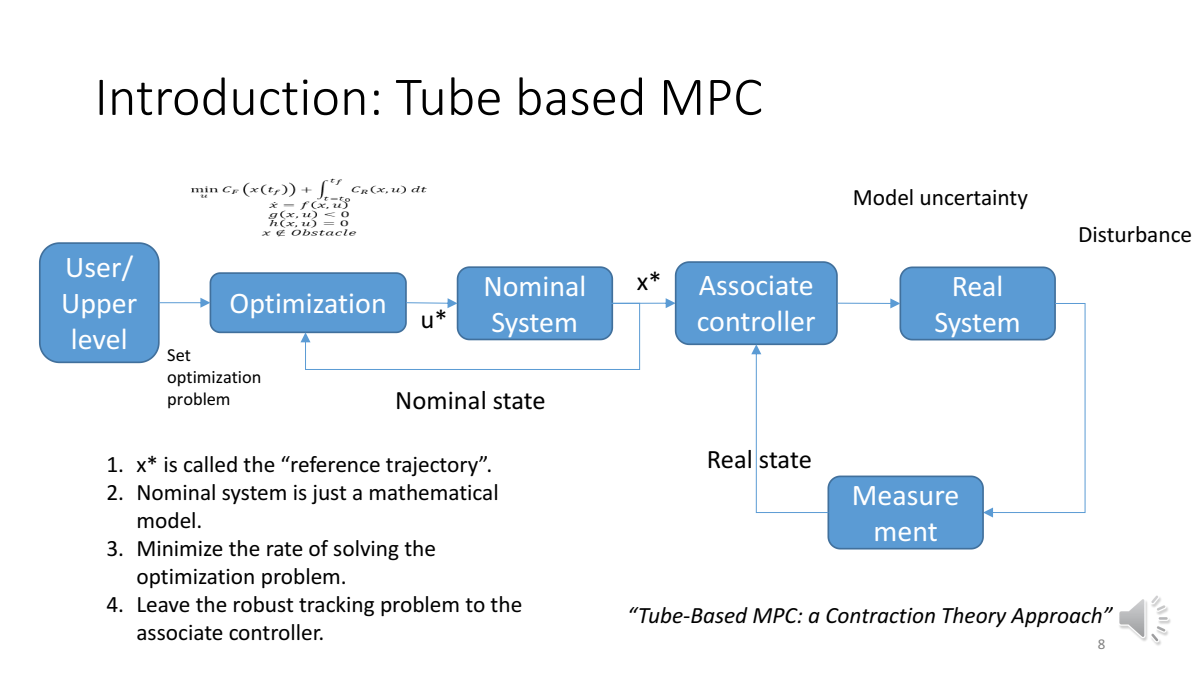
Tube based MPC相较于RHC新增了Nominal System（相当于$u^*$用于输出参考轨迹$x^*$）和Associate controller（相当于参考轨迹$x^*$作为目标状态用于控制实际状态）

由于Nominal System只是数学模型，因此$x^*$是理想的；跟踪的鲁棒性问题（Model uncertainty和Disturbance）全都由Associate controller决定

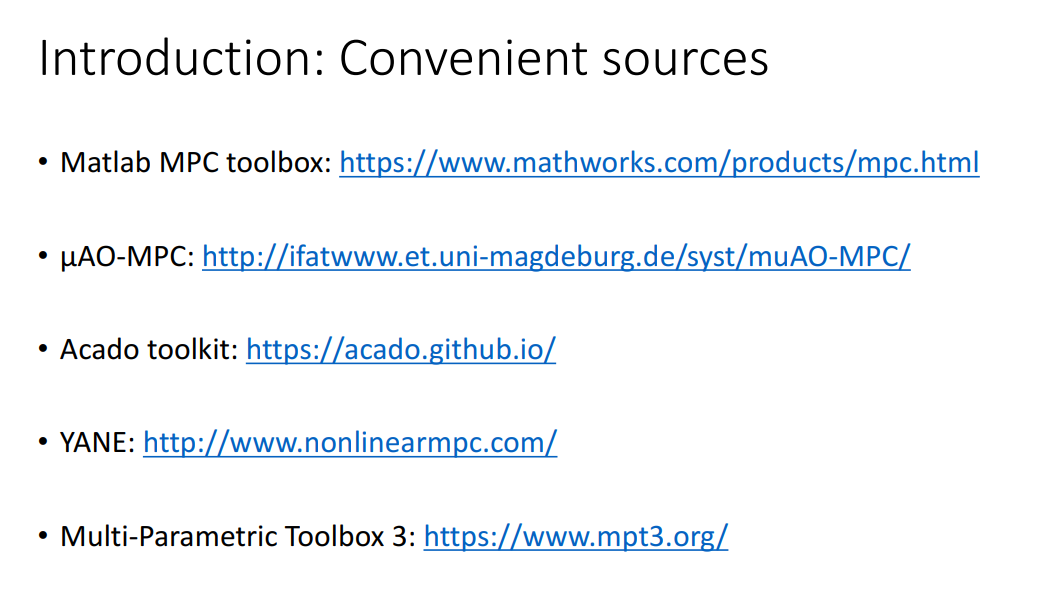
求解MPC的一些工具

Linear Model Predictive Control（MPC）

建立系统模型

这里的控制量为jerk，4s内离散化为20份（通过离散，参数化J）。可以将离散的P、V、A表示为向量形式（并建立与向量J的关系）

这个表达式可以用离散状态转移方程推导得到

💡 离散状态空间方程

递推得到离散状态转移方程

💡 模型预测控制：主要用于跟踪已知轨迹。

它的当前最优输入$u^*$是在每一个采样瞬间通过求解一个有限时域开环最优控制问题而获得。当前状态作为最优控制问题的初始状态，解得的最优输入序列只实施第一个最优输入$u^*$。

比如车跟踪一个直角折线时，使用MPC就能考虑到转折之后的状态，从而以一个较平滑的弧线跟踪

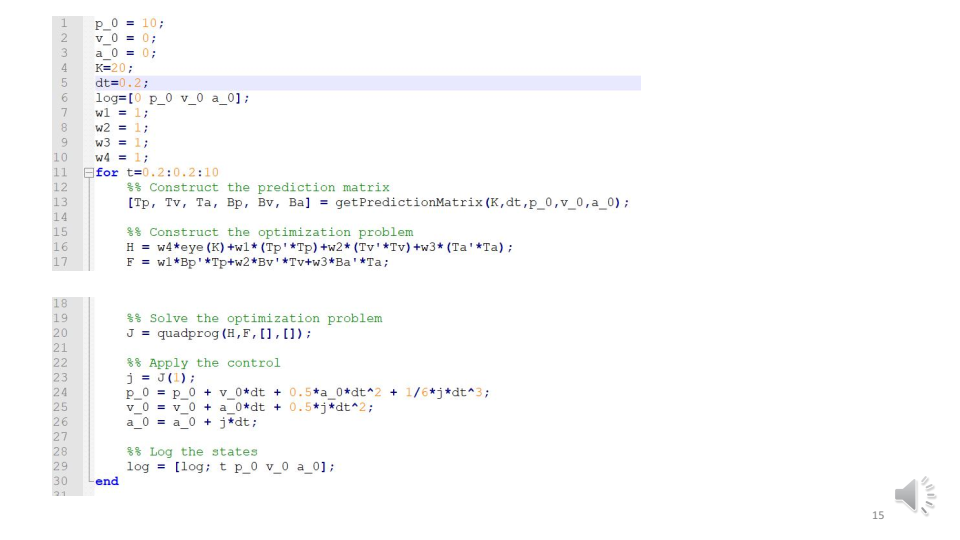
软约束——加入惩罚函数，优化问题数值求解（不在是二次规划问题）

💡 加入L后，仍能保证问题为凸优化问题

当v满足约束范围时，L=0即可最优化（$\omega_5$为一个极大的值，若L>0会，目标函数会变得很大）

当v超过约束范围时，L则只有大于0才能满足不等式约束（$-T_vJ≤1_{20\times 1}+B_v+L$）,此时最优控制$u^*$会尽量使L变小——即使v满足约束条件

状态约束——一般使用软约束，状态一般受测量噪声和干扰的影响，故有可能超出预定范围

输入约束——一般使用硬约束

Non-linear MPC

Jerk Limited trajectory

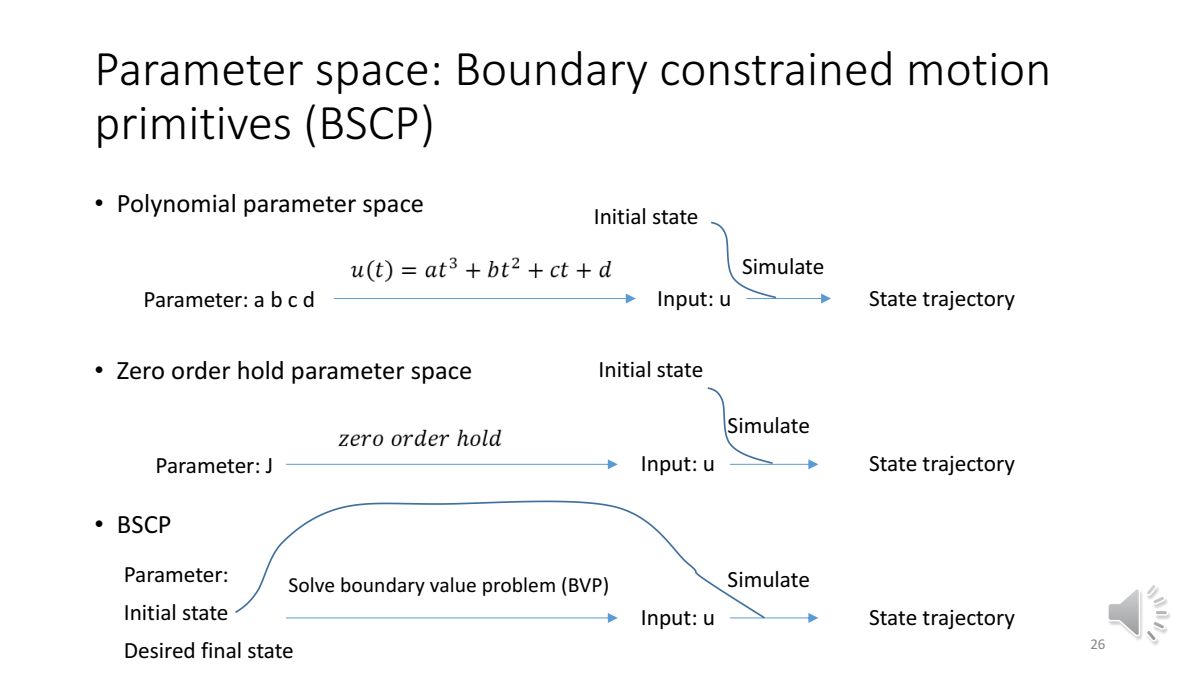
参数空间：多项式参数空间、零阶保持器参数空间、BSCP（Boundary constrained motion primitives）——参数：系统的初末状态，通过解一个BVP问题，得到输入$u$（最后可以优化的参数相当于是系统的末状态）

BSCP中一种用得比较多的类型：JLT（Jerk Limited Trajectory）

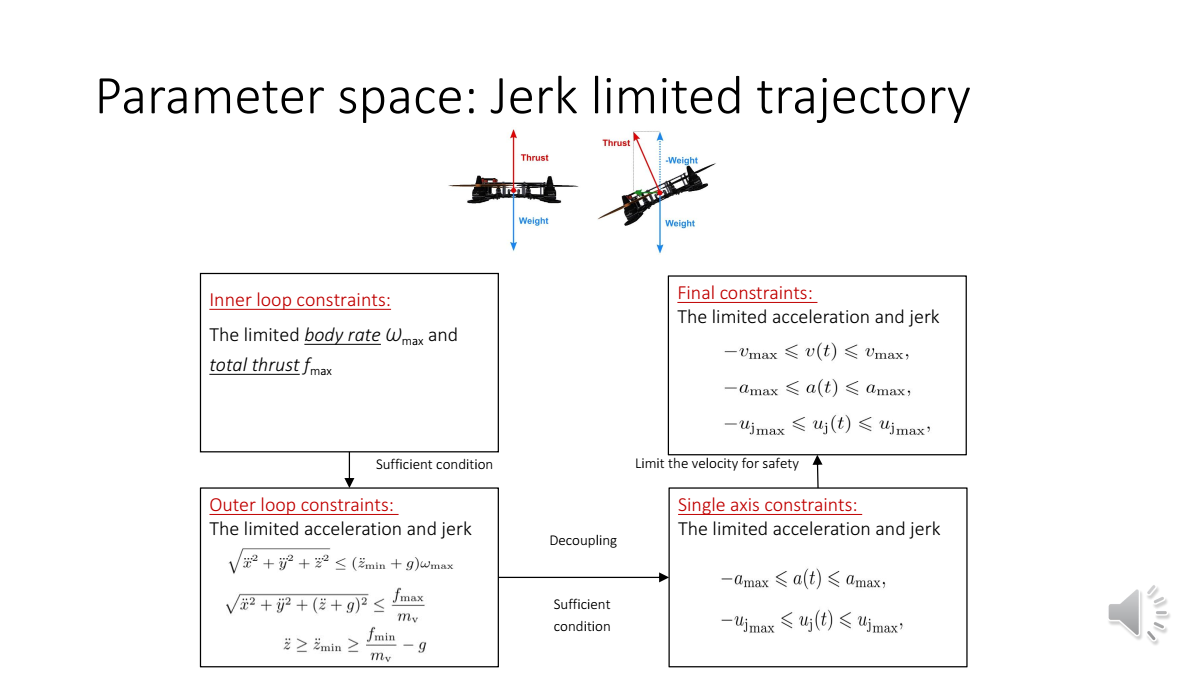
无人机内环约束（$\omega_{max}$和$f_{max}$）转化为外环约束

先推导二阶的情况（到达目标速度）

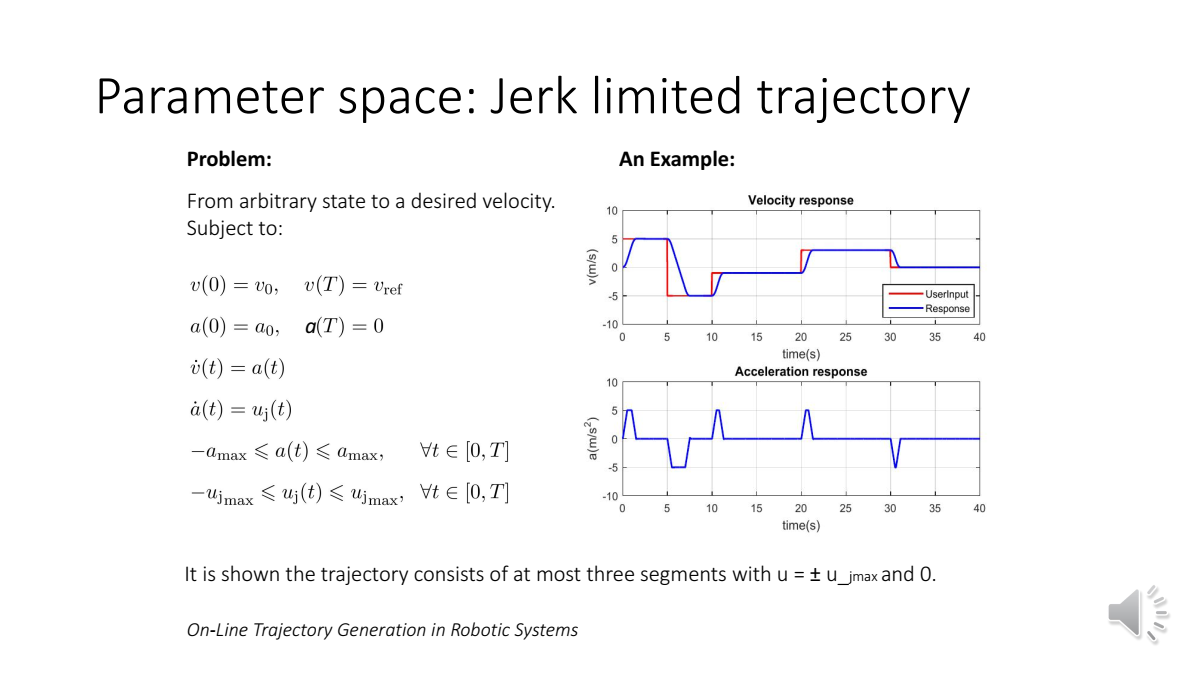
轨迹最多包含三段$u=±u_{max}$and$0$的情况 （详情见：On-Line Tranjectory Generation in Robotic Systems）

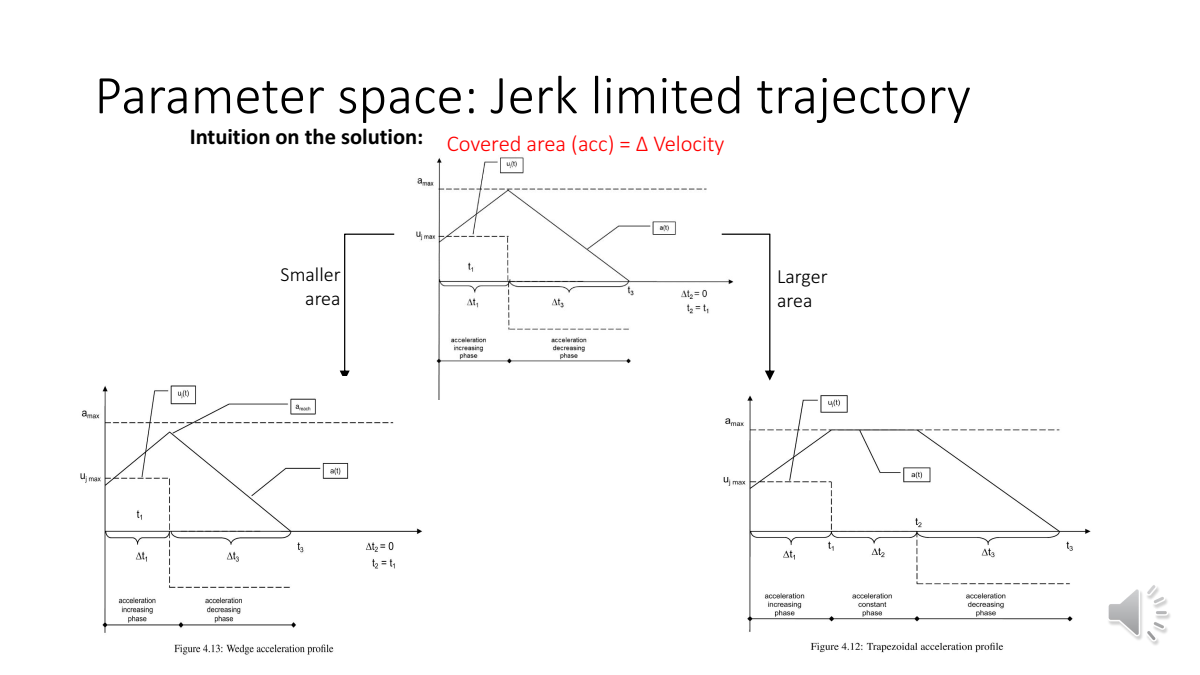
当$v_{ref}>v_0$时，先取$u=u_{max}$，当$a$达到$a_{max}$时，取$u=-u_{max}$，使$a_t=0$。$a$与$x$轴围成的面积即为$\Delta v_0$，若$\Delta v=v_ref-v_0>\Delta v_0$，larger area——围成梯形面积，维持在$a_{max}$一段时间；若$\Delta v=v_{ref}-v_0<\Delta v_0$，smaller area——实际达不到$a_{max}$。进而可以得到输入$u$

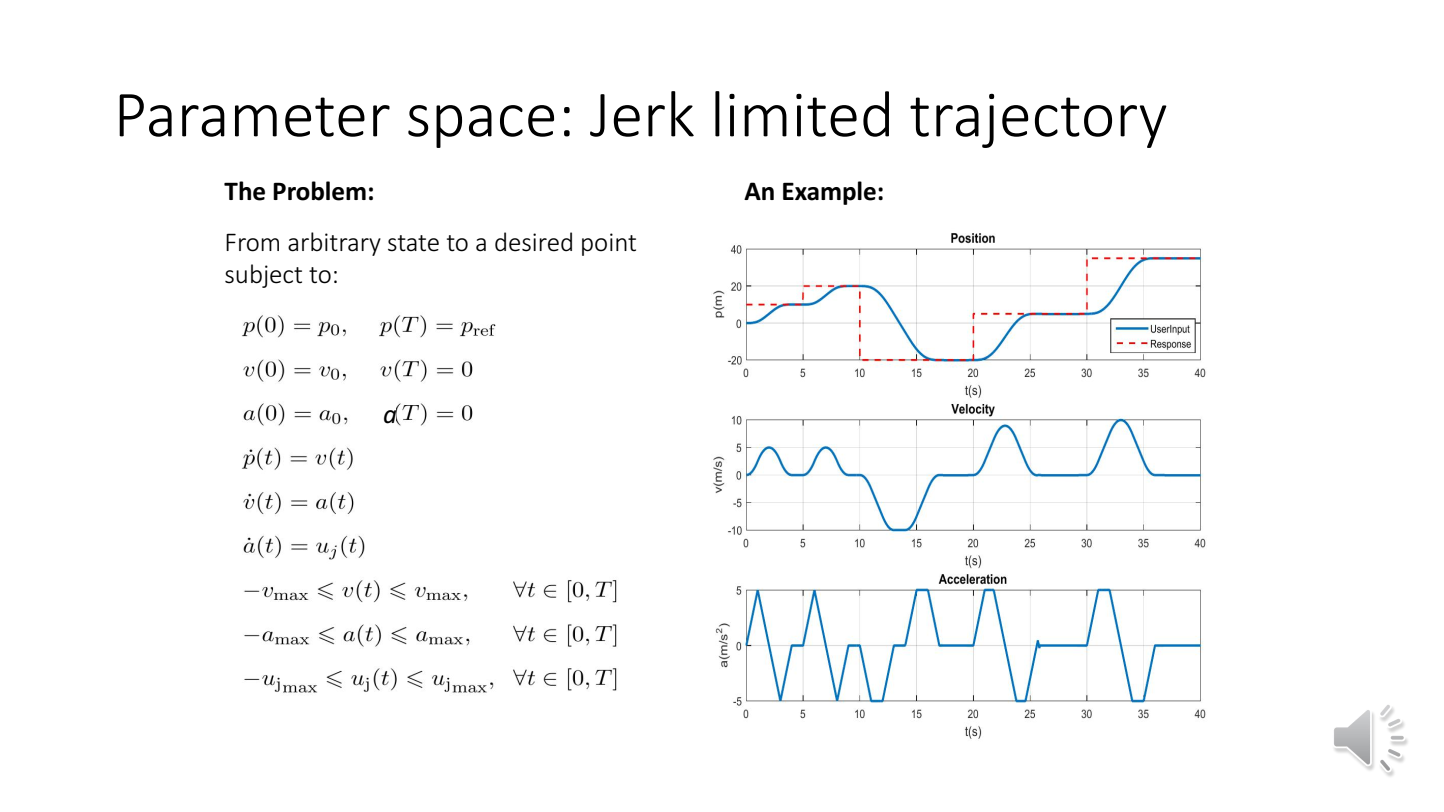
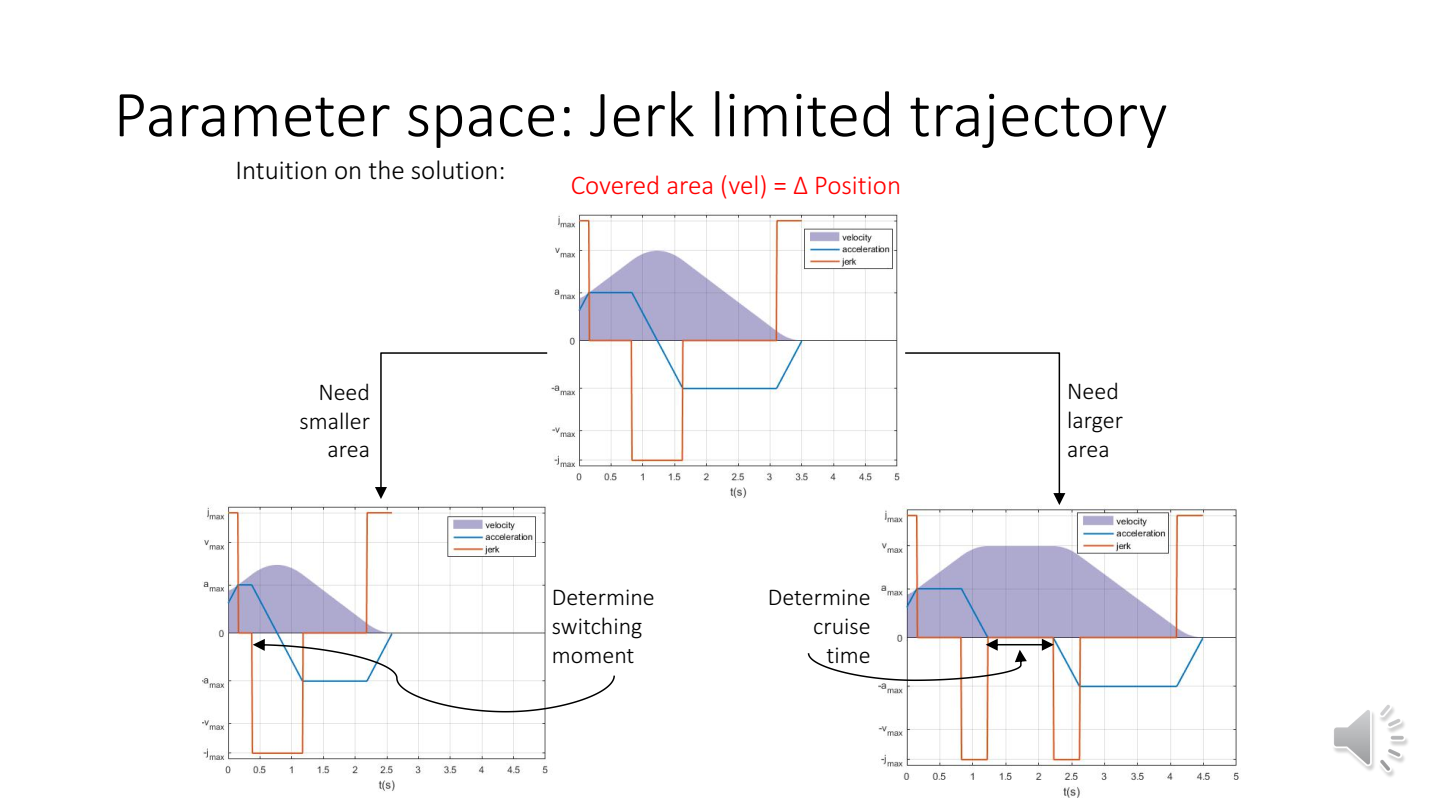
和只含v、a的二阶情况类似，含p、v、a的三阶情况是让v到最大速度，然后再让v回到0。根据这种情况下所围成的面积$\Delta p_0$和实际的$\Delta p$大小，可以求得输入$u$的表达式

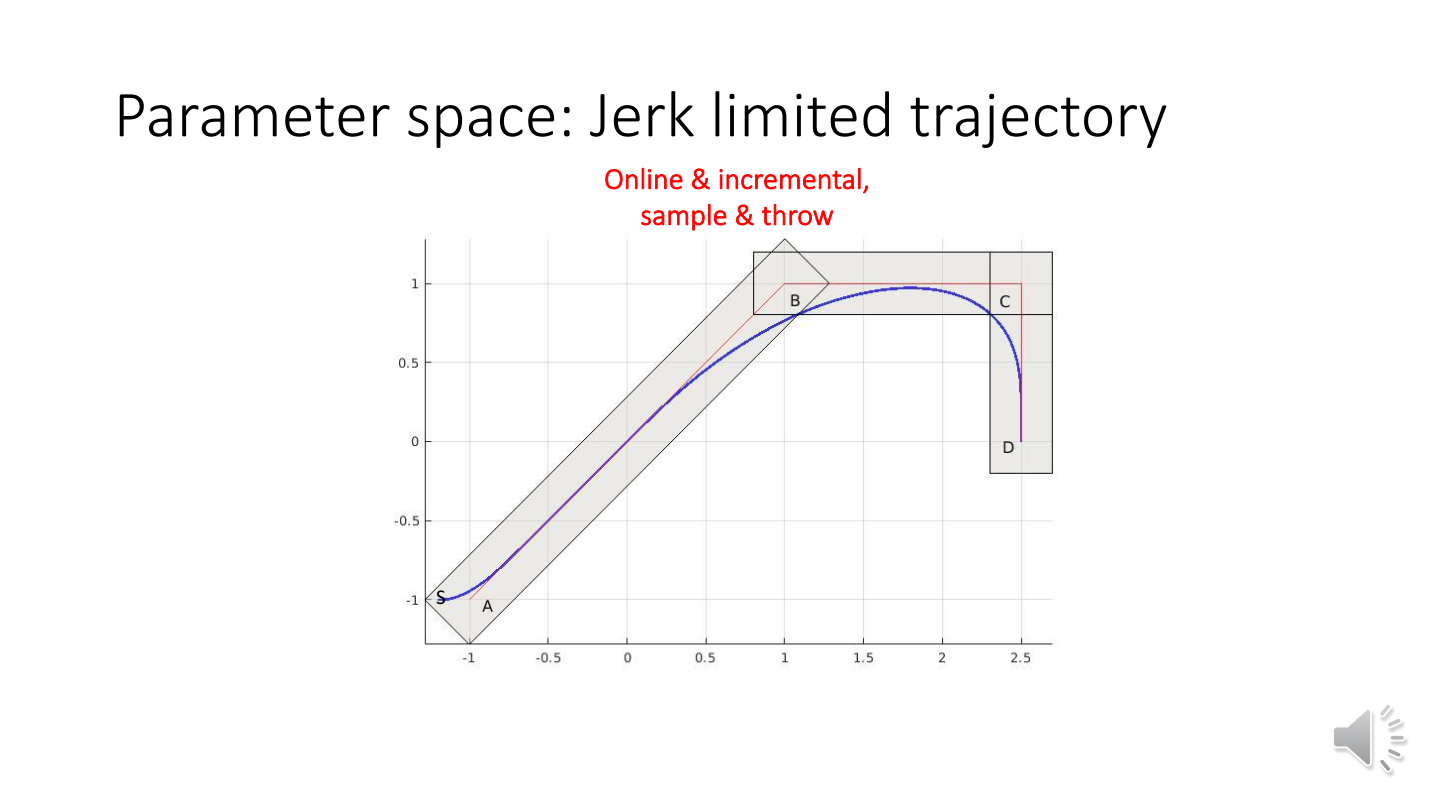
JLT+安全走廊——可以快速生成轨迹

首先生成一条从A到B的轨迹1，无人机沿着轨迹1飞行；每隔一段时间生成从当前点到C点的轨迹2，并判断轨迹2是否在安全走廊内——不在，抛弃该曲线；在，无人机跟随新的轨迹。重复

也可以二分法（查看从轨迹1中点到C点的轨迹是否在飞行走廊内部），一次性生成完整轨迹

Non-linear MPC

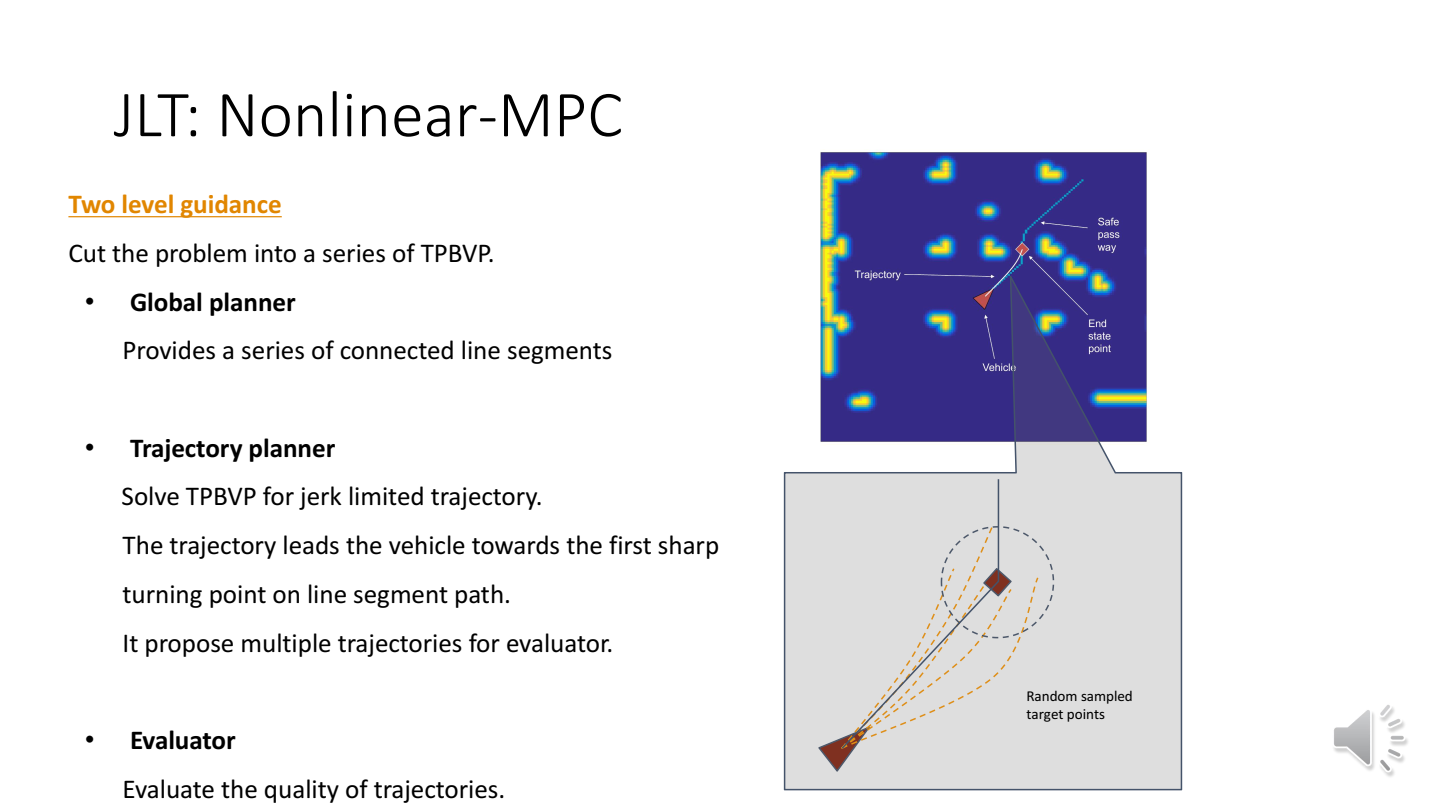
非线性MPC一般是用做局部规划器。

• 全局规划器：提供一系列连接的线段——A*、JPS…

• 局部规划器（轨迹规划器）：求解JLT下的two-point boundry value problem

  💡 JLT下一个参数空间下的末状态$x_f$能求解出对应轨迹$x(t)$和输出$u(t)$。

  局部规划器在全局规划器的拐点附近采样得到一组末状态$X_f$，求解出每组末状态对应的轨迹，并评估出最优的轨迹

• 评估器

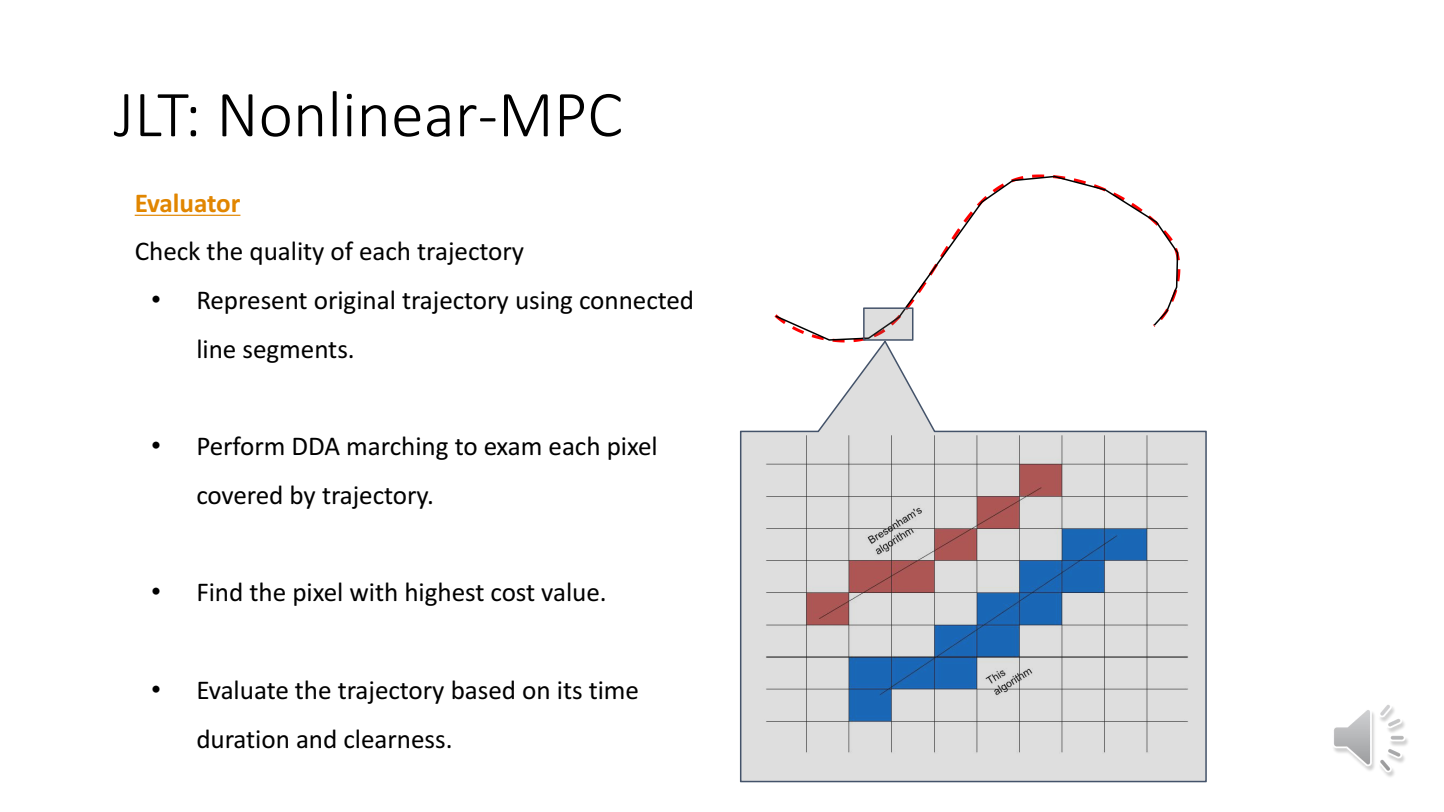
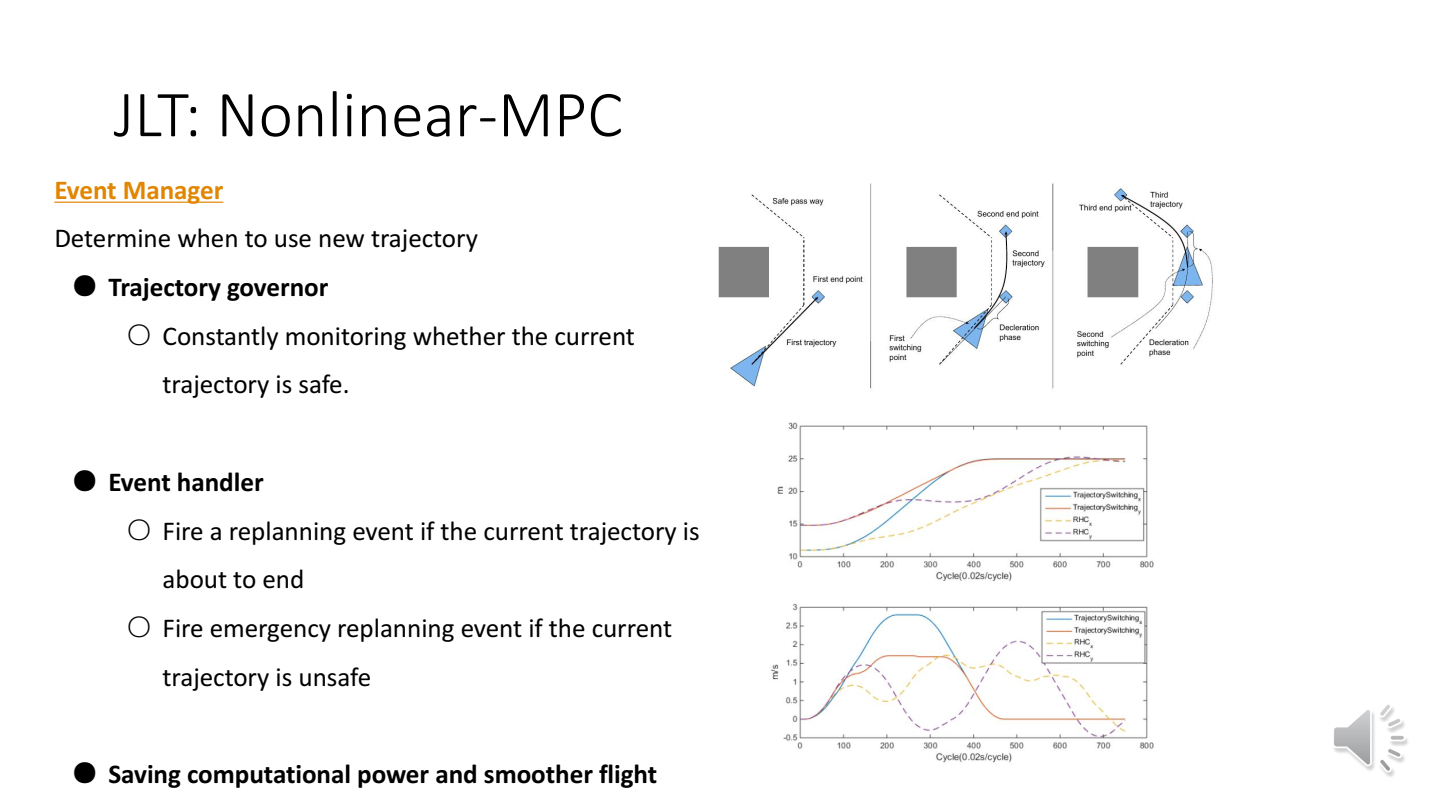
普通的MPC会每隔一小段时间计算一次输入$u^*$。这往往会导致算力消耗过大，并且使生成的轨迹不平滑。而事件驱动型MPC只有当必要时才进行MPC重新计算，往往配合Tube based MPC使用（即有一个Associate controller控制轨迹）

必要情况：MPC生成的轨迹快跟踪完了，轨迹上有障碍，全局规划器路径变化

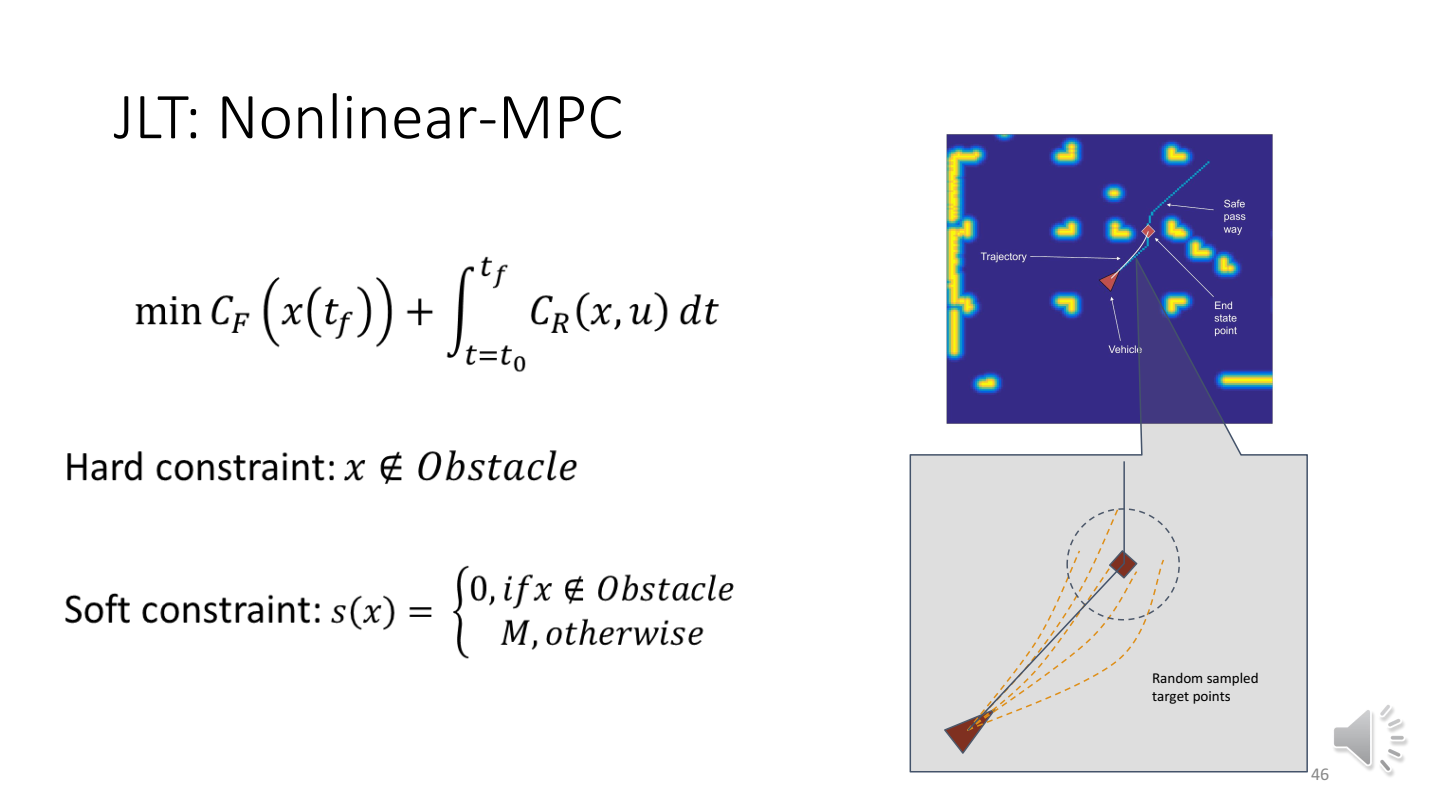
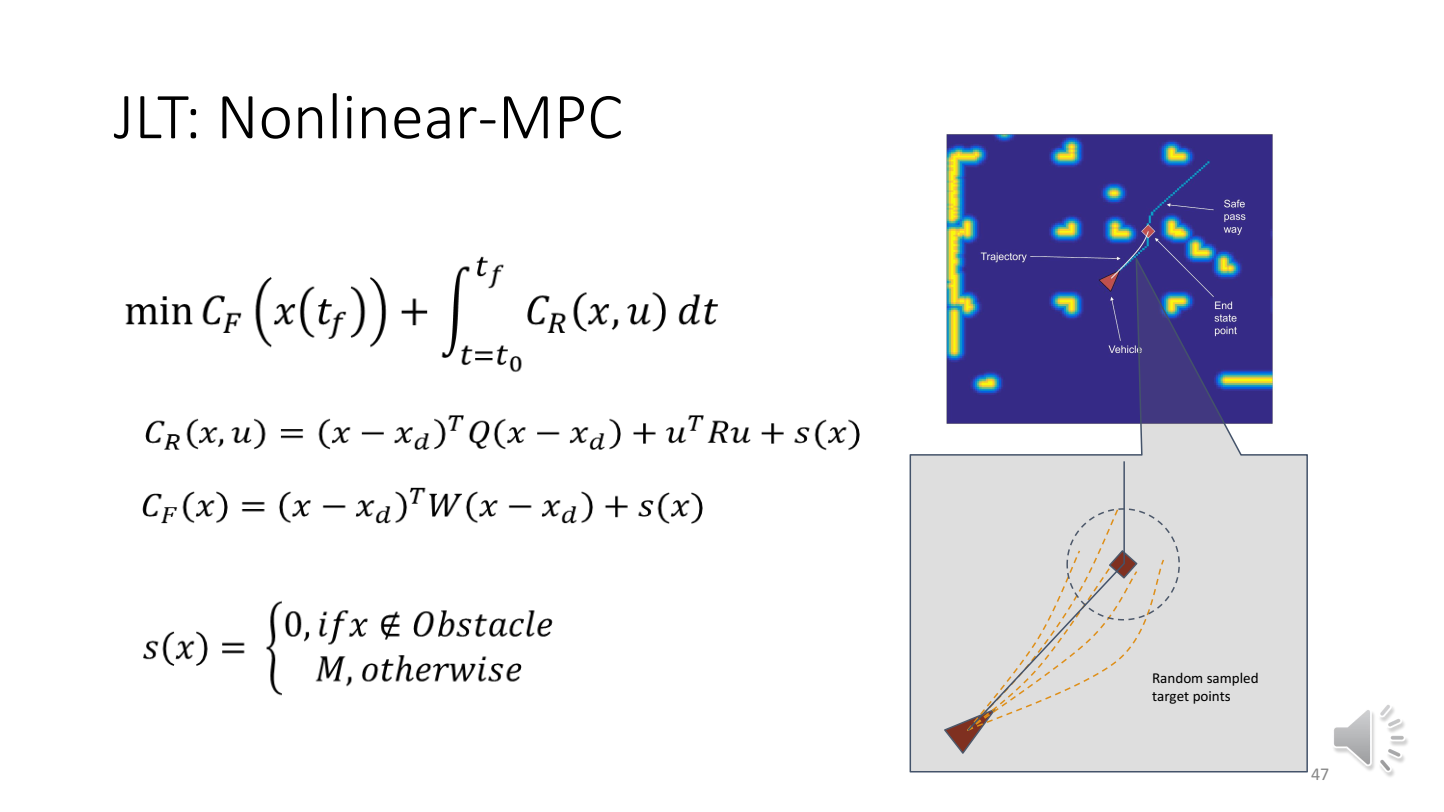
由于JLT已经天然地满足$\dot x=f(x,u)$，$g(x,u)<0$，$h(x,u)=0$，优化时仅需要考虑障碍物的约束。硬约束、软约束

当使用软约束（s(x)有很强的非线性）并随机散点时，目标函数往往是不具备梯度信息的。因此，需要使用不需要梯度信息的优化方法——如粒子群优化（Particle swarm optimization）

PSO的每轮迭代的采样点（粒子）按照一定法则运动，最终收敛到最优的点附近

粒子每轮迭代的运动都沿速度方向

更新粒子的速度方向：考虑上一次迭代的速度方向，考虑朝全局最优的方向移动（全部粒子中的代价最小的粒子），考虑朝自身迭代历史中最优的方向移动

新的粒子速度方向为上述三个速度向量的求和（对每一项加上一个权重和随机数rand）

💡 JLT只能用于系统模型是三阶积分器的情况！！对无人车等不太适用

General BSCP

对于General BSCP，通常需要求一个数值解（一个$<x_0,\theta>$对应一个$<\hat u,\hat x,\hat t_f>$（参数为$\theta$））。该优化问题同样为离散的形式——可以使用PSO

若直接使用PSO，则一次采样需要求解一次General BSCP问题（数值解）。而PSO优化又需要大量的采样，因此会导致计算速度慢，实时性差

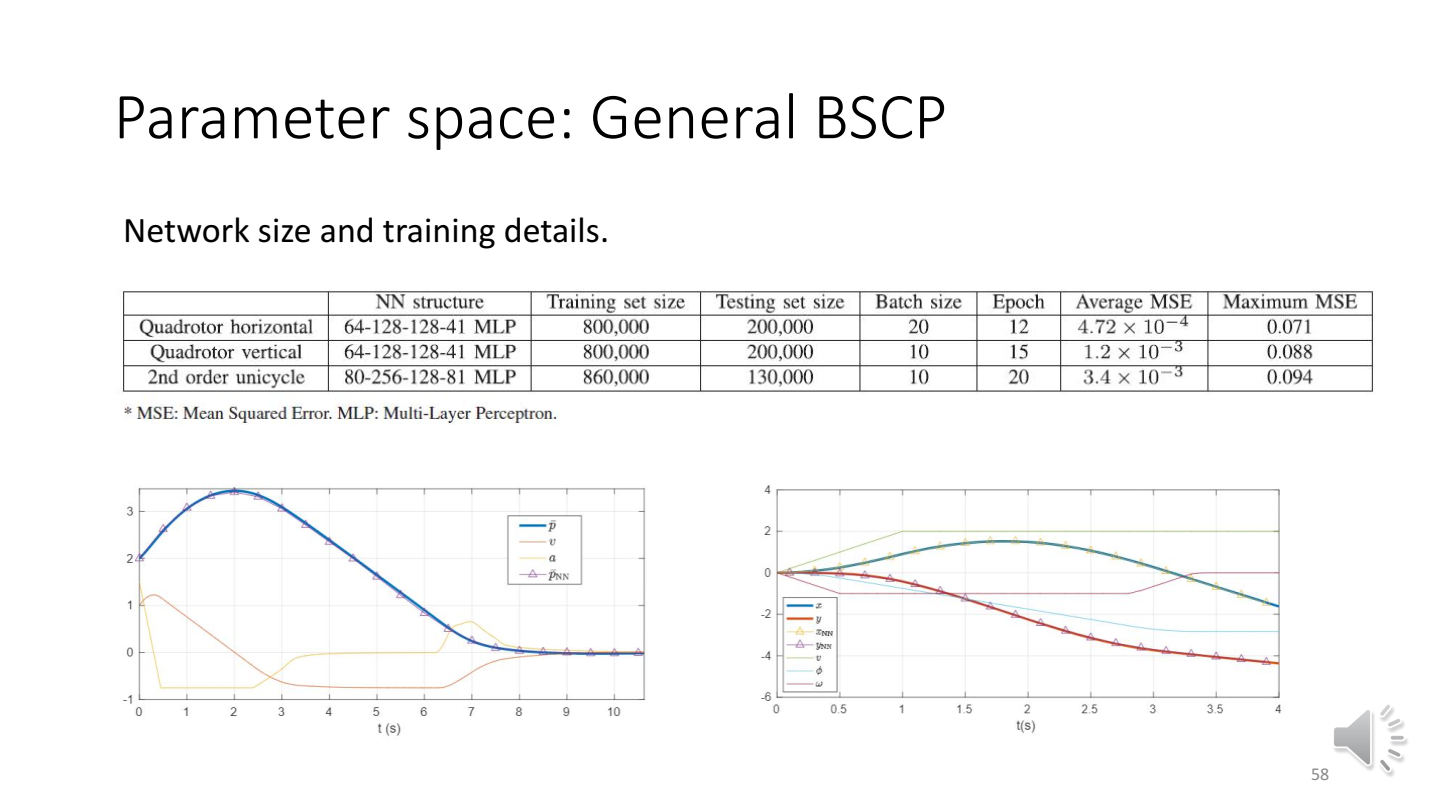
给定输入$<x_0,\theta>$，通过神经网络得到$<\hat u,\hat x,\hat t_f>$，不需要多次求数值解。最后得到最优的参数$\theta^*$——可以用网络得到$u^*$或者求数值解保证精度

神经网络估计梯度信息

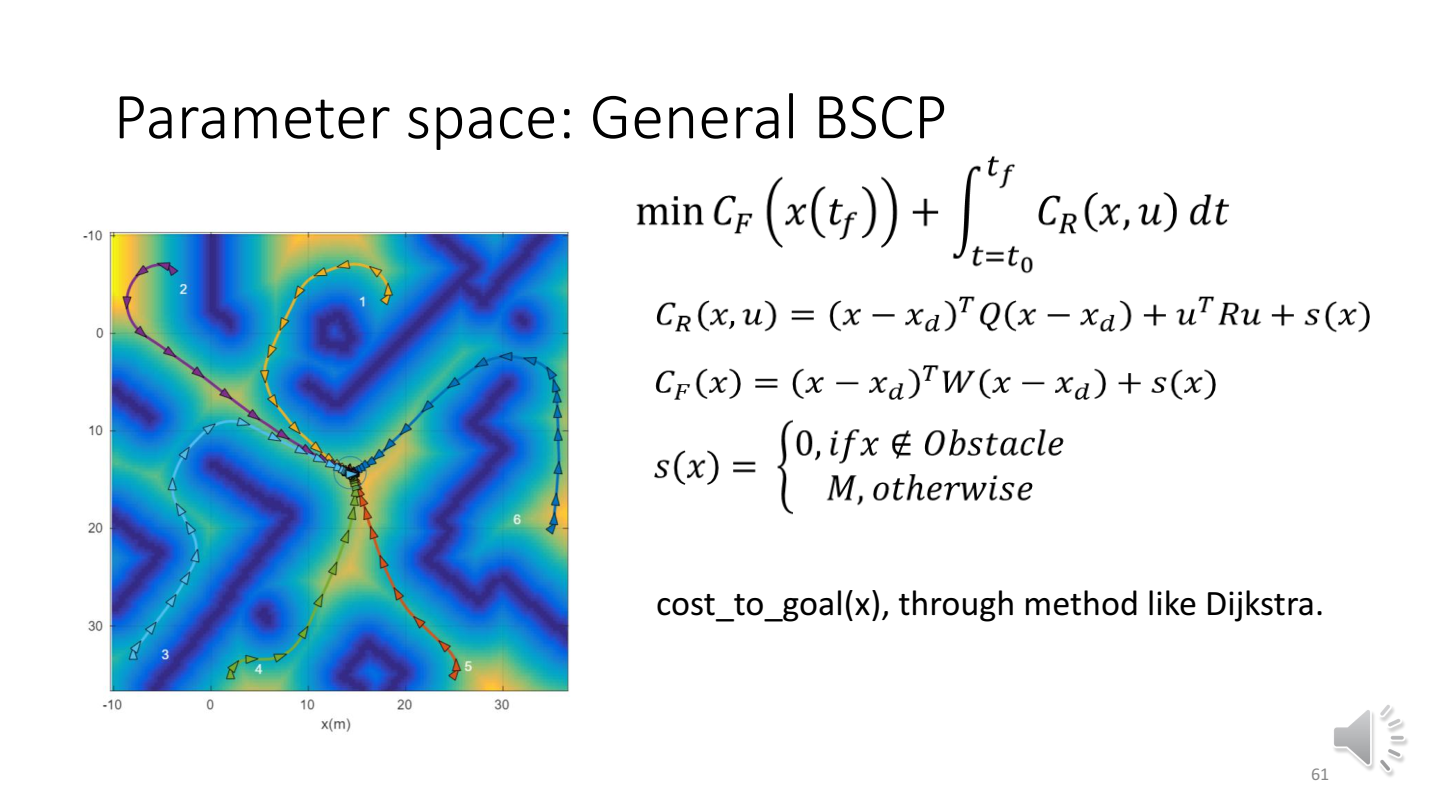
使用$x-x_d$容易陷入局部最优（可能会使轨迹卡住），因此可以采用Dijkstra等方法得到全局最优