运动规划

基于马尔科夫决策过程的运动规划

Planning with Uncertainties

在实际应用中，机器人的执行和状态估计都存在不确定性

不确定的分类：nondeterministic（不知道不确定性的来源）、probabilistic（机器人能够估计不确定性）

两种Game的方式：

函数L为代价函数

在nature参与的情况下，寻找最优的planning

One-step Analysis：

One-step Worst-Case Analysis：nondeterministic的模型下，执行 $u$ 时受到的 $\theta$ 是未知的。因此，认为每步nature可能采取最坏的策略干扰robot，选择让代价函数最大值最小的u
One-step Expected-Case Analysis：Probabilistic的模型下，Independent Game的概率 $P(\theta)$ ，Dependent Game的概率 $P(\theta|u)$ 是已知的。因此，选择让代价函数L的期望最小的u

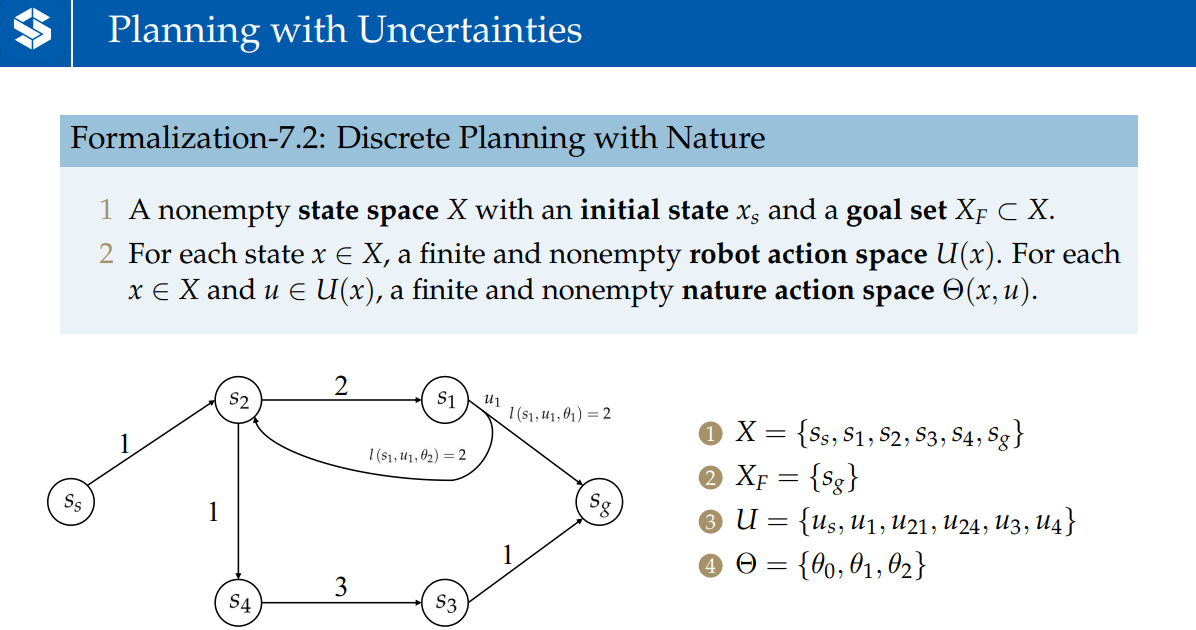
状态空间 $X$ ，目标状态集 $X_F$ ，robot action space $U(x)$ ，nature action space $\Theta(x,u)$

状态传递函数 $f(x,u,\theta)$

离散的情况——状态集 $X_{k+1}$ ；连续的情况—— $P(x_{k+1}|x_k,u_k)$ 相当于所有在 $\theta_k$ 作用下到达 $x_{k+1}$ 情况的概率 $P(x_{k+1},\theta_k|x_k,u_k)$ 的求和

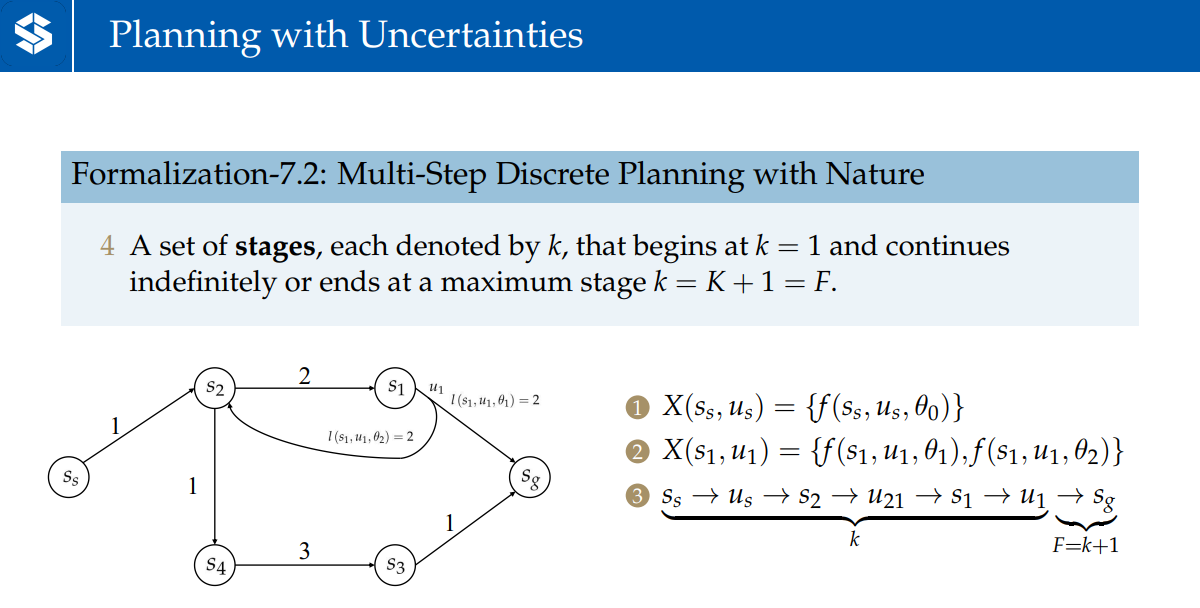
一个stage表示从起点状态到目标状态的一系列过程（这个过程有k+1个状态 $x$ ，k个输入 $u$ ）

planning with uncertainties的定义

$l(x_k,u_k,\theta_k)$ 表示单步的代价函数

马尔科夫决策定义了状态转移函数 $P(x_{k+1}|x_k,u_k)$ 和即时激励函数 $R(x_k,x_{k+1})$ ——相当于单步的代价函数

难点：如何把问题构建成一个MDP模型，示例如下：

3相当于状态传递函数 $f$ 为 $x_k+u_k$ 在 $\theta$ 影响下所形成的高斯分布

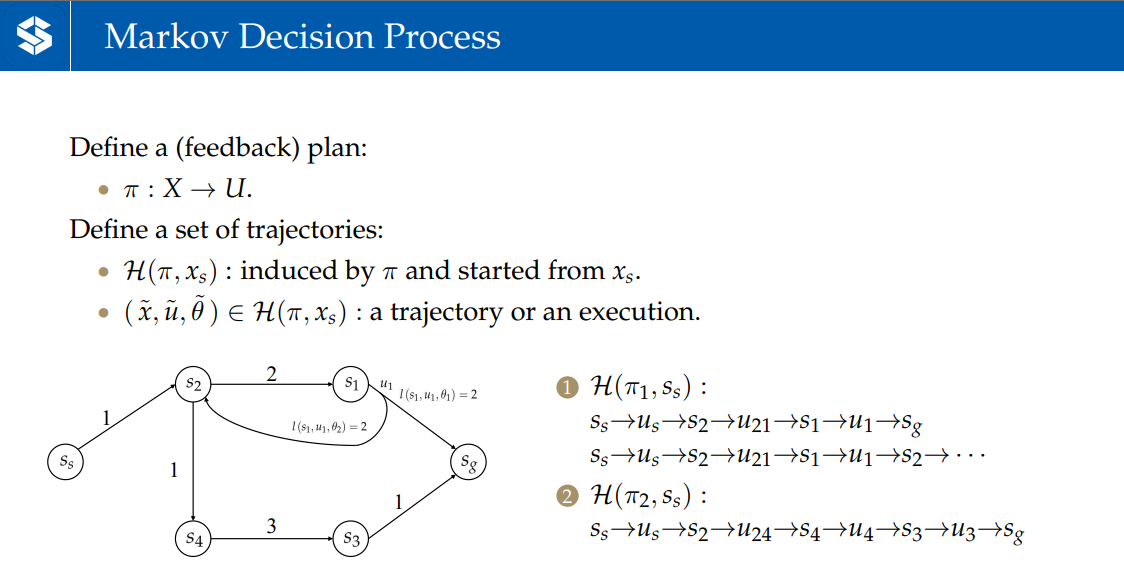
$\pi$ ：规划状态 $X$ 下应该执行的动作 $U$

$H(\pi,x_s)$ ：由 $\pi$ 诱发的从起点的终点的trajectory集合

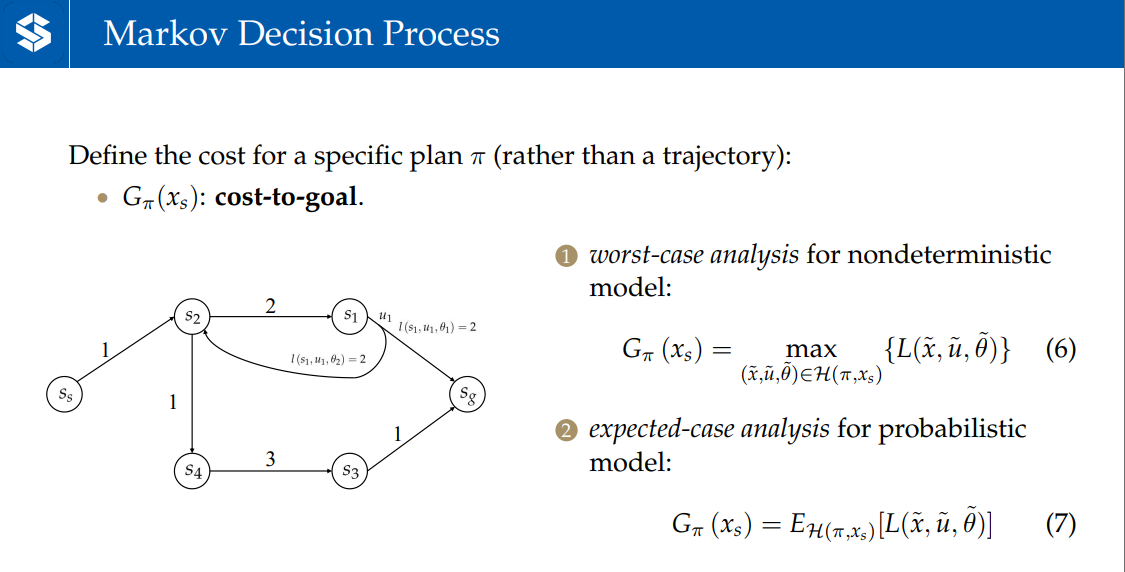
$G_{\pi}(x_s)$ 表示到目标点的代价。对于nondeterministic的模型，G等于所有诱导出的trajectory中代价最大的trajectory的代价；对于probablistic模型，G等于所有诱导出的trajectory的代价取平均

直接求解较麻烦，用动态规划（Dynamic Programming）建立优化问题——寻找第k步和第k+1步的optimal plan的递归关系

$x_K$ 表示终末状态的前继节点状态

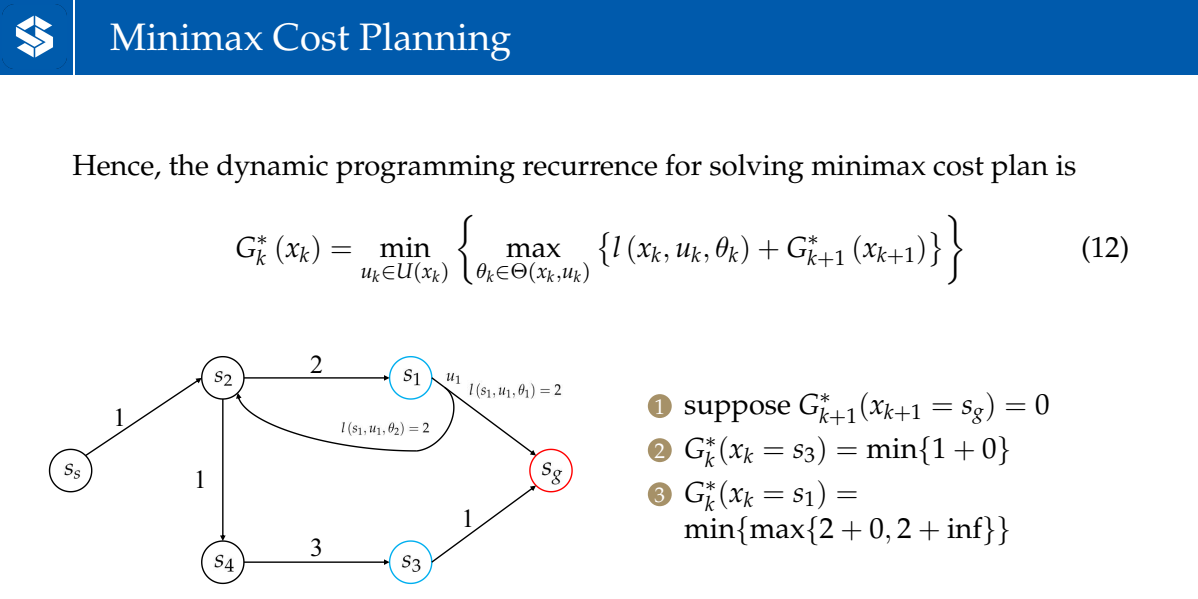
$G^*_k$ 中有一项含inf是因为，在未遍历到的情况下， $G^*(x)$ =inf

和Dijkstra算法类似（ $u_k$ 能使状态从 $x_k$ 到状态 $x_{k+1}$ ，相当于能否通过 $u_k$ 使 $G(x_k)$ 变小）

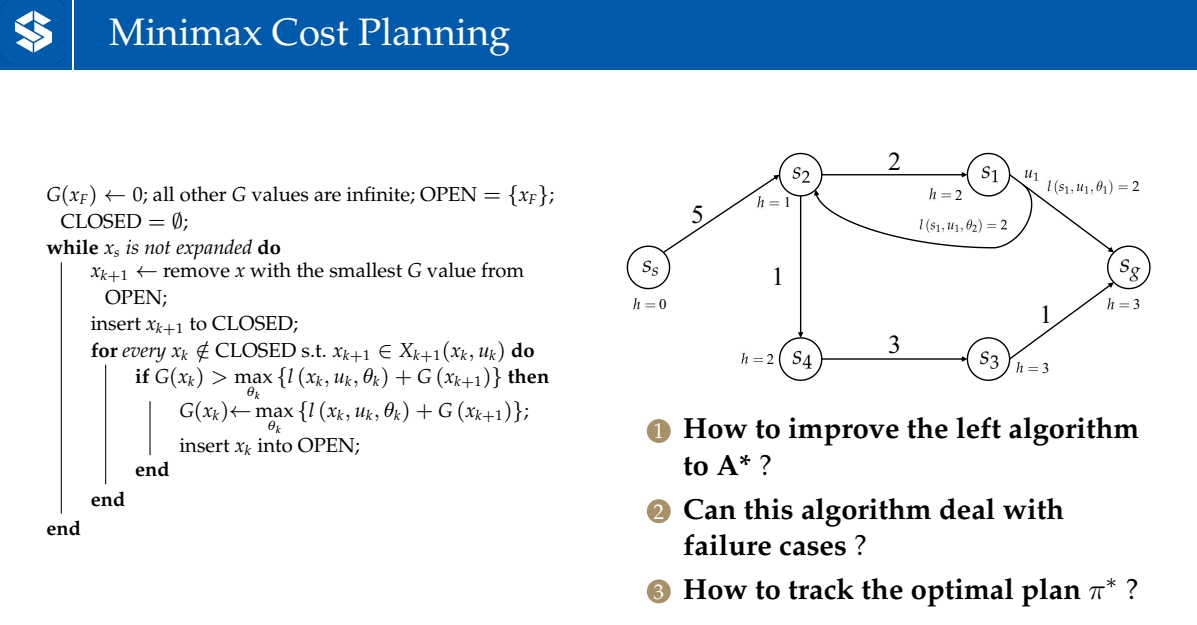
1：将该算法improve to A*：用当前节点到起点的距离作为启发式函数（如图中所示， $s_1$ 到 $s_s$ 的启发式函数为2—— $s_1$ 到 $s_s$ 至少要经过两步）

2：对于failure case，如图中的 $s_1$ 、 $s_2$ ， $s_2$ 先拓展之后进入闭集， $s_1$ 便无法和 $s_2$ 形成循环，拓展之后也进入闭集

3：存储每个状态 $x_k$ 下应该选取的 $u_k$

优缺点：对不确定性的鲁棒性强；但过于悲观，且计算较困难（最终得到一个决策树）

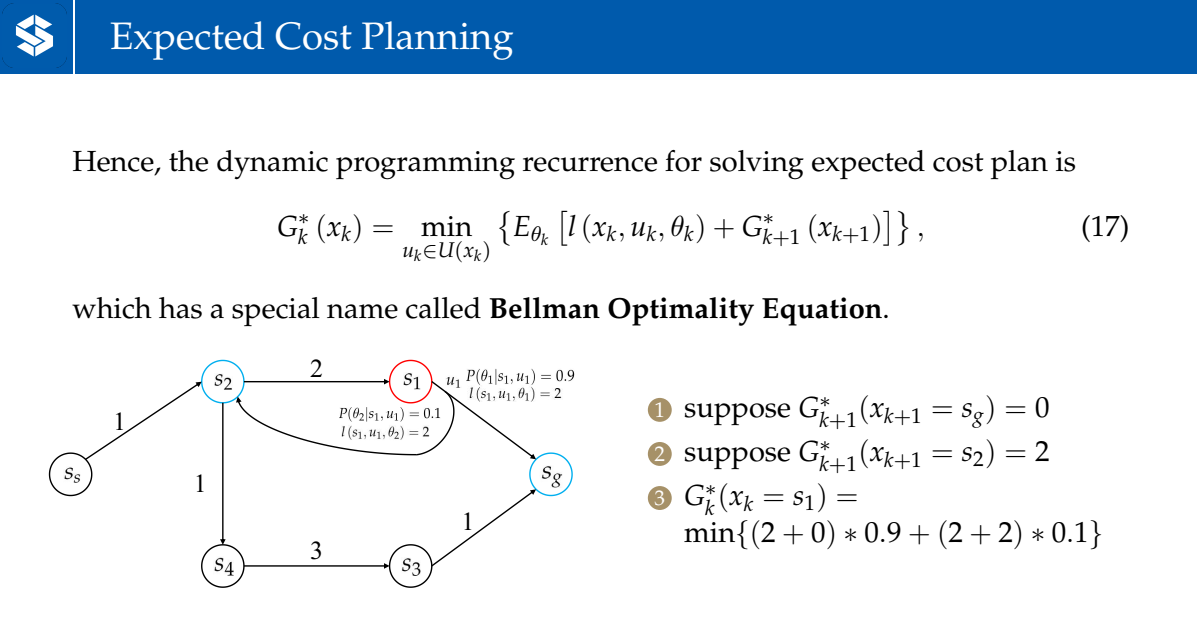
Except Cost Planning和Minimax Cost Planning的 $G^*(x_k)$ 的递推类似

Bellman Optimality Equation

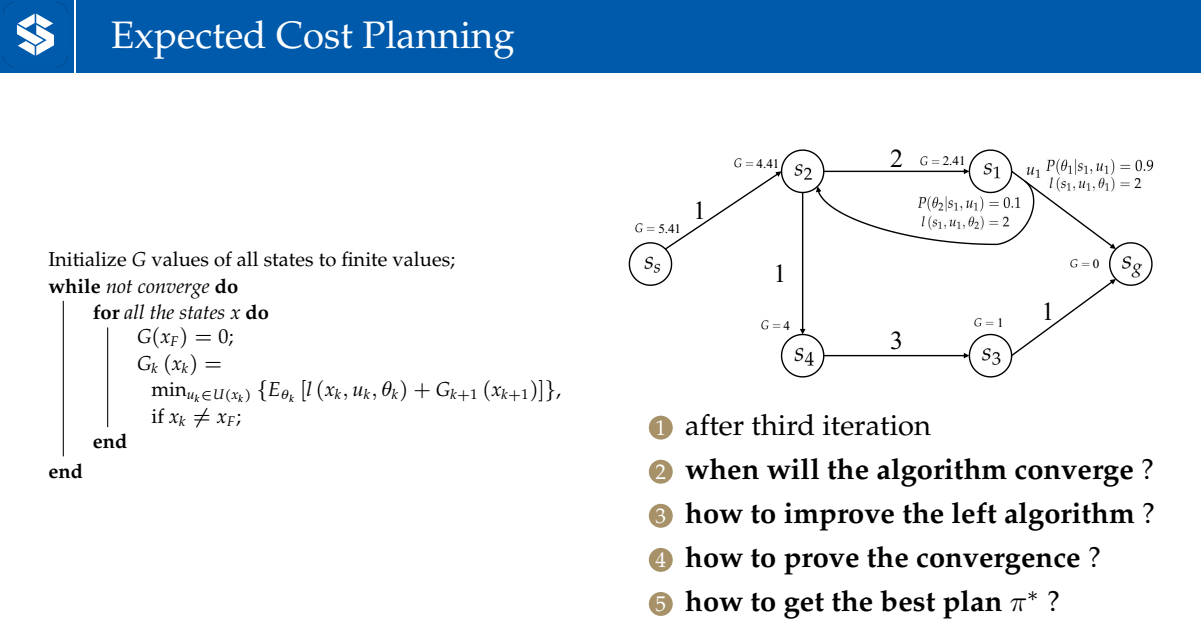
概率最优（单次的执行并不一定是最优的）

用admissible values（小于真实cost的值）去初始化G值
从起点开始，遵循贪心策略（判断可达节点中哪个节点的 $G+l$ 值最小，选该节点作为后继节点），直到找到一条达到目标的轨迹
更新轨迹上的所有状态节点的G值
重复2—4步，直到当前贪心策略生成的轨迹上的所有的状态都满足Bellman errors< $\Delta$ ， $\Delta$ 为本次G值和上一次G值之差的绝对值