硬约束及软约束下的轨迹优化
概述
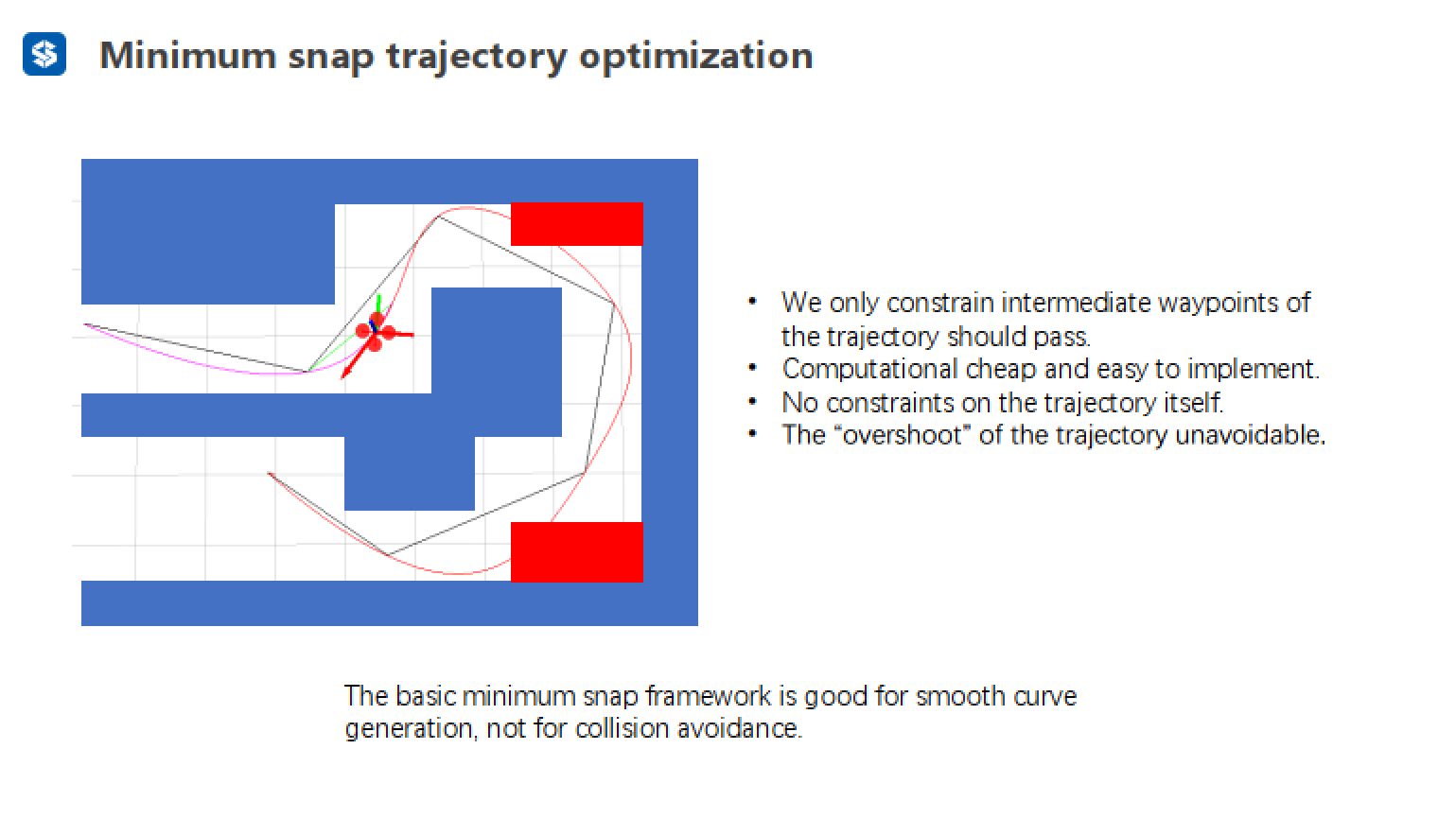
Minimum snap的优缺点:
-
优点
- 轨迹一定会经过中间路点
- 可以闭式的求解出轨迹上每一处的状态信息
- 构造了一个凸优化问题,可以闭式和数值求解
-
缺点
可以生成平滑的轨迹,但没有考虑避障
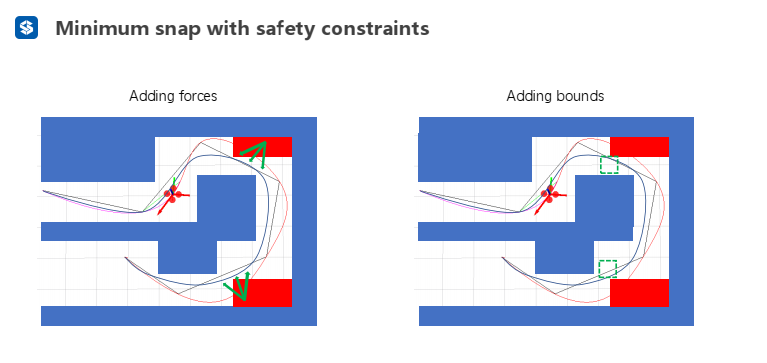
解决方法:
- Adding forces:添加推力或吸力,使轨迹往远离障碍物的地方拉——软约束
- Adding bounds:添加区域约束,使轨迹必须处于区域当中——硬约束
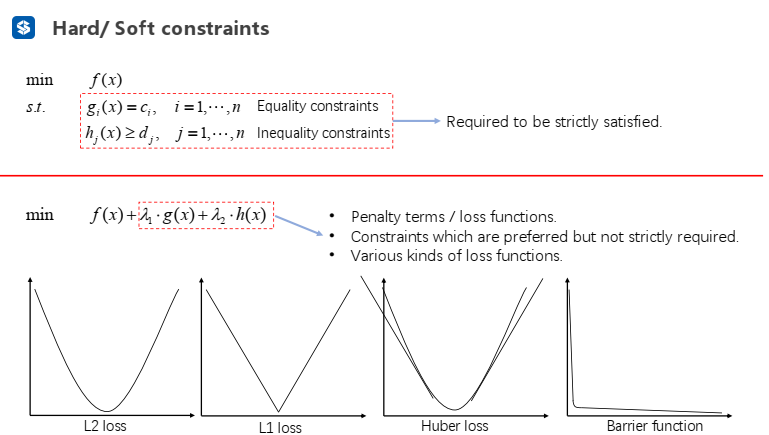
硬约束——相当于给优化问题施加一些等式或不等式的约束,要求轨迹必须严格地满足约束
软约束——相当于给优化问题加上惩罚函数(比如靠近障碍物时,惩罚函数就会增大),不一定严格地满足约束
惩罚函数常见形式:二次函数(L2)、一次函数(L1)、Huber function(L1+L2)、Barrier function(例如,靠近障碍物时,惩罚函数的值会急剧增大)
硬约束优化
基于走廊的轨迹优化
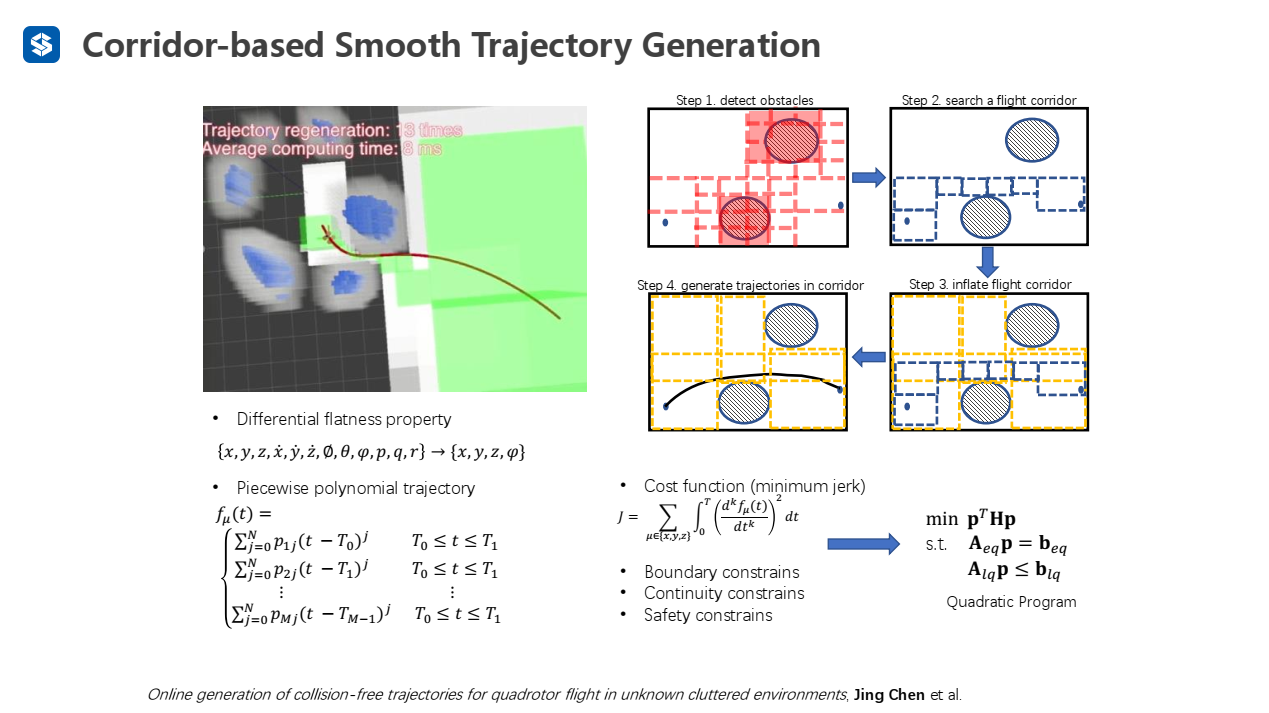
步骤:
- 探测障碍物,生成八叉树地图
- 生成一个飞行走廊,利用前端的路径规划方法
- 膨胀飞行走廊
- 在飞行走廊中生成轨迹
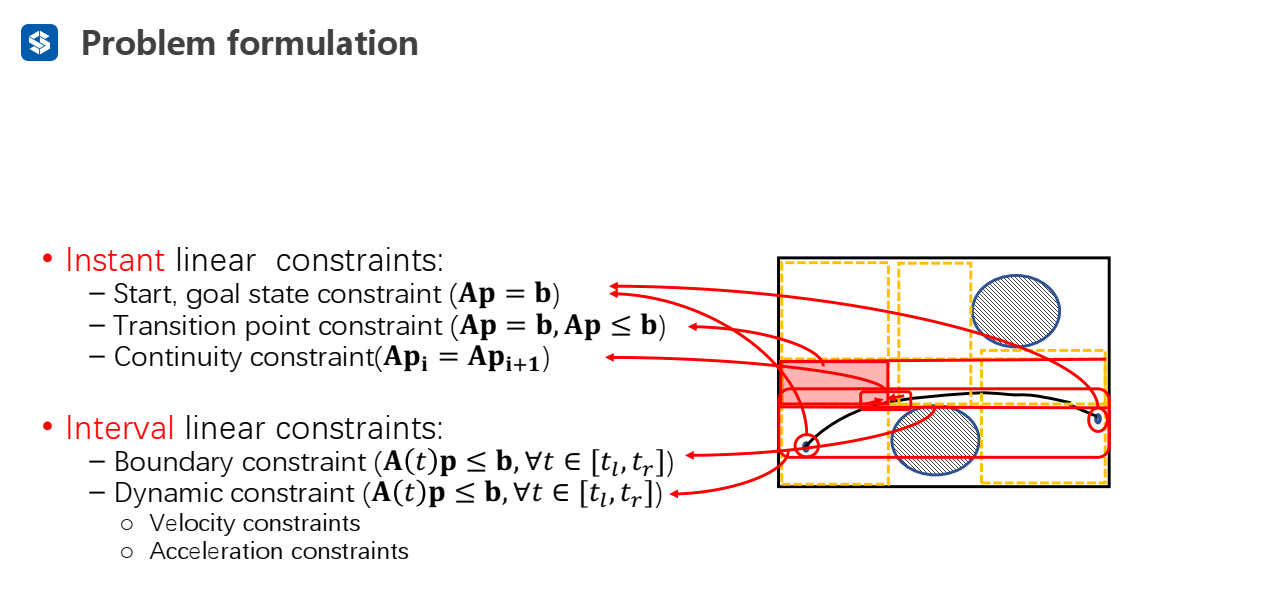
施加的约束:
-
Instant linear constraints:
- 起点、终点的状态约束
- 两段多项式轨迹交界点的约束(在两个飞行走廊的交界处)
- 连续性约束
-
Interval(区间) linear constrains:
- 边界约束(保证轨迹在飞行走廊内)
- 动力学约束
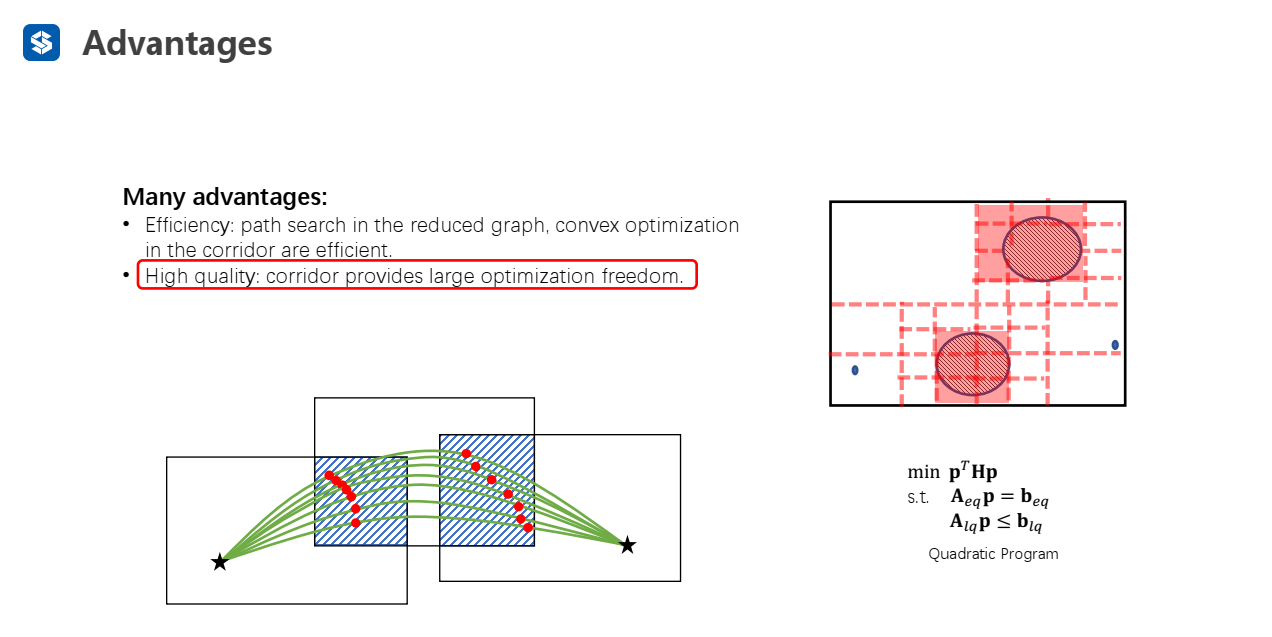
飞行走廊提供了很大的优化的自由:两段轨迹交界点可以在两个飞行走廊的交界区域移动(提供了一定的优化空间),进而可以使时间分配更加合理(中间段分配时间长——可以让中间段的两个端点在走廊交界区域进行调整)
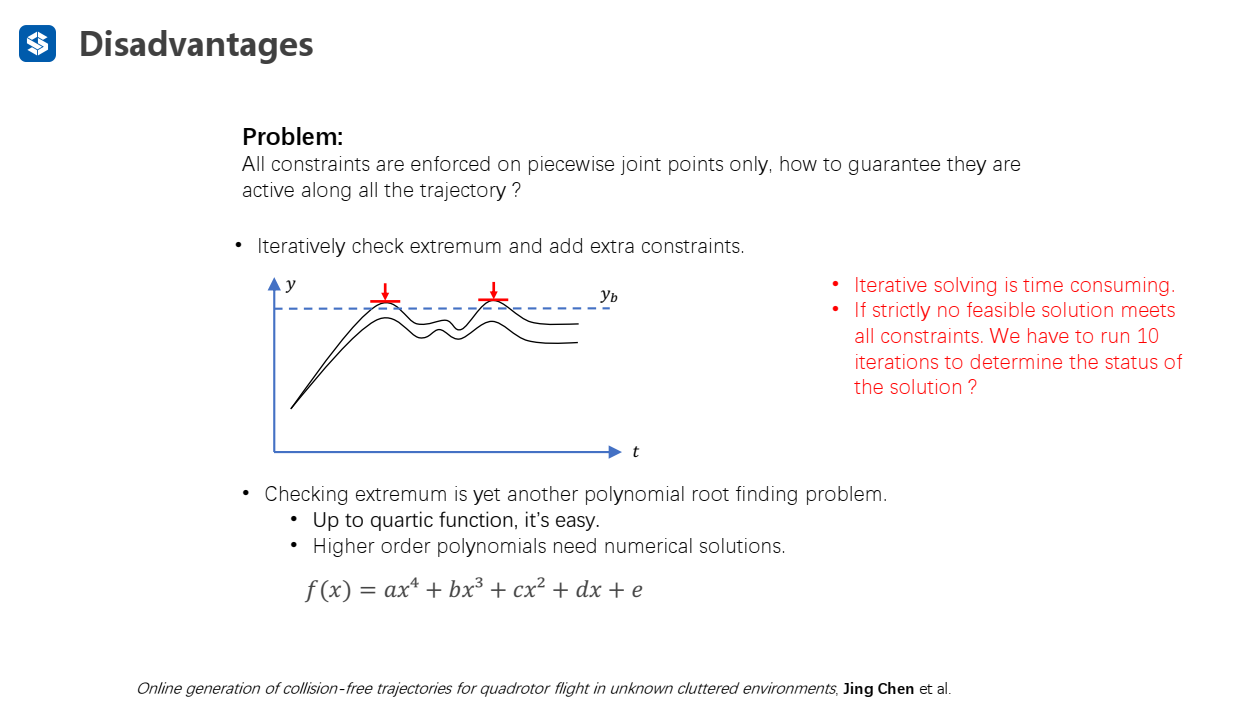
后验检查——迭代地检查极值点——如果不满足则时间额外的约束(在极值点的位置施加一个约束(),之后再进行检查)
贝塞尔曲线优化
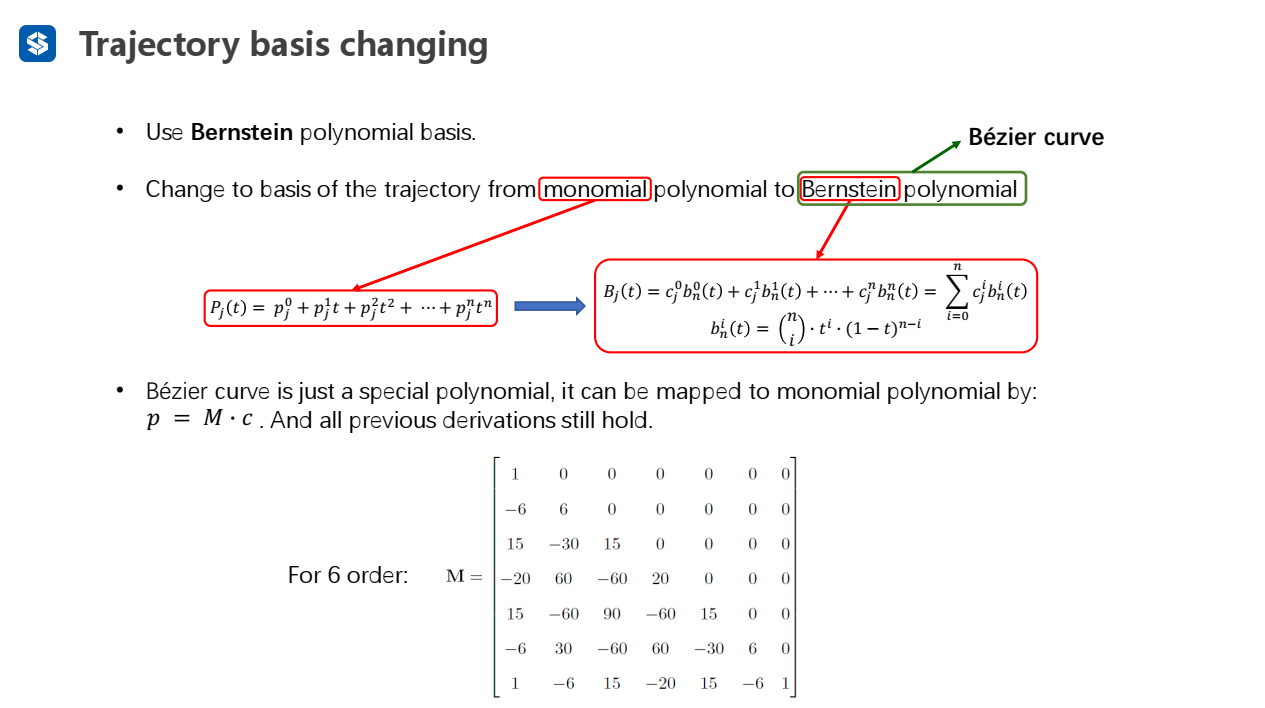
Bernstein多项式:其中,系数表示控制点
对于Bernstein多项式,一定能映射成普通多项式(可以用矩阵表示,)
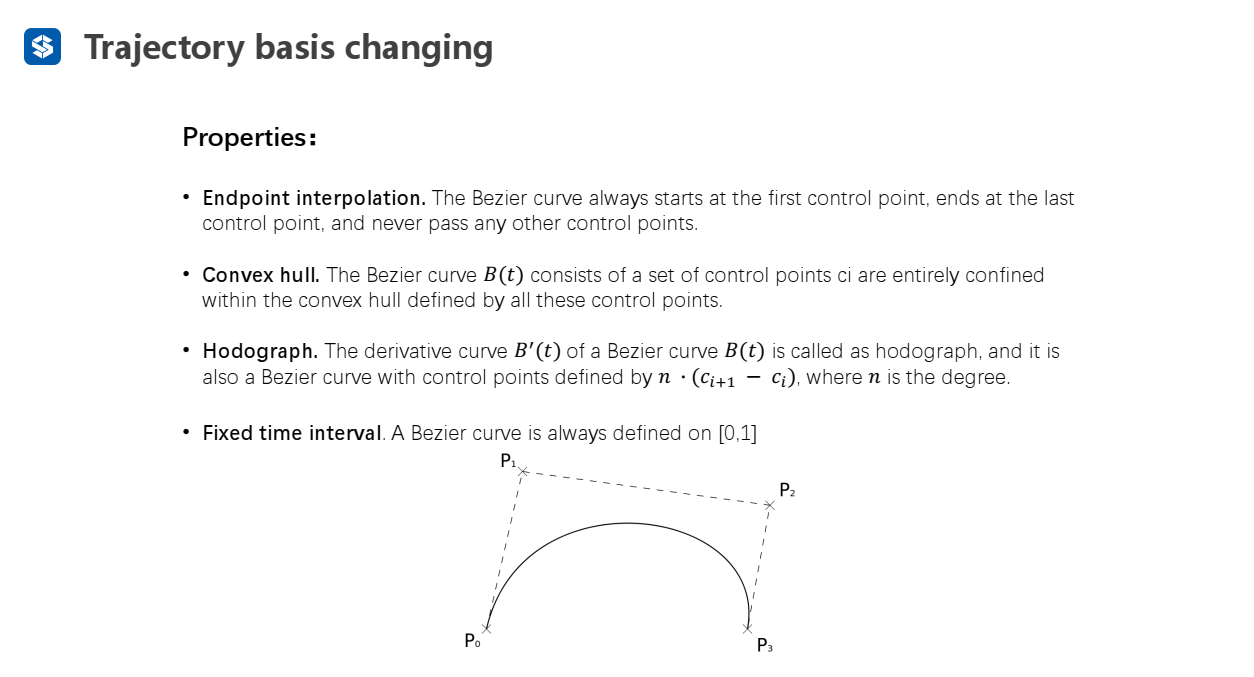
贝塞尔曲线的特性:
- Endpoint interpolation(插值):贝塞尔曲线一定经过第一个控制点和最后一个控制点,不会经过中间其他控制点
- Convex hull(凸包):贝塞尔曲线被包含在控制点构成的凸包内
- Hodograph:贝塞尔曲线导数的控制点可以表示为
- Fixed time interval:只能被定义在,使用时需要将时间映射到
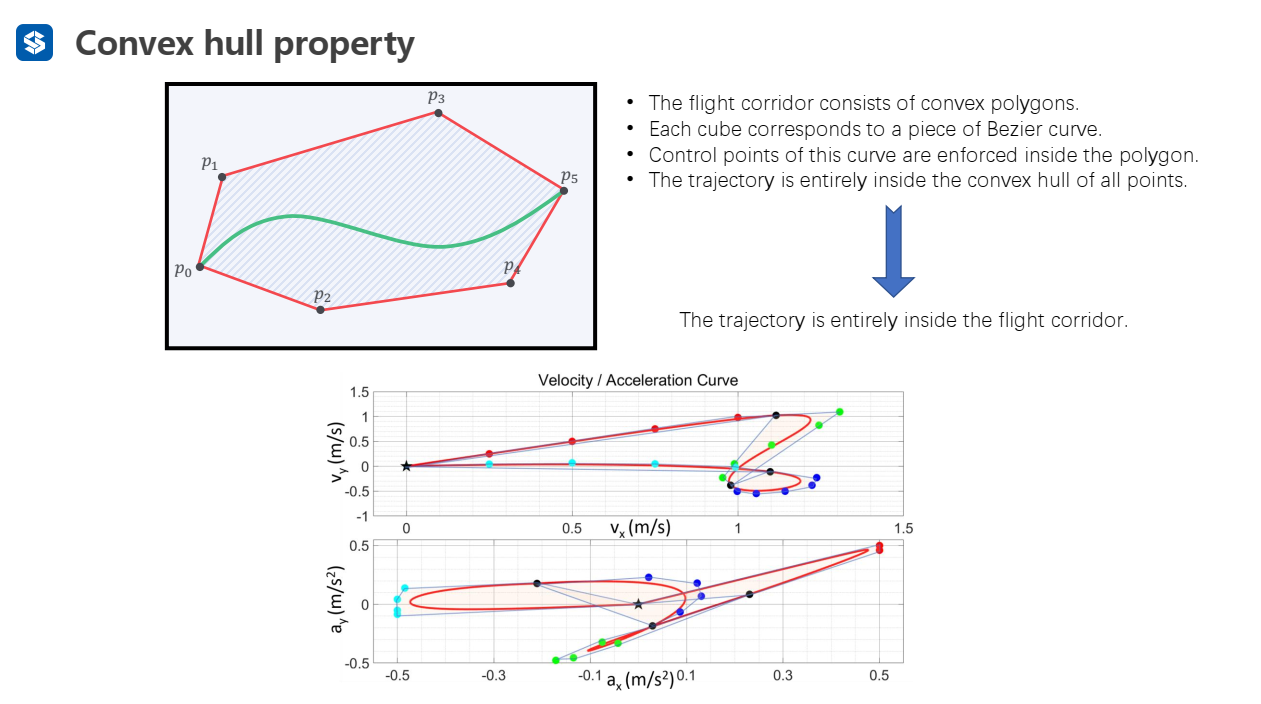

表示的次方
对于边界约束和连续性约束,都施加在分段贝塞尔曲线的首端或末端,因此可以直接以简单的形式表示出约束(如上图所示)
PS:上图中表述应该有问题,应该是,得到一个递推表达式
Other Options
Dense constrains
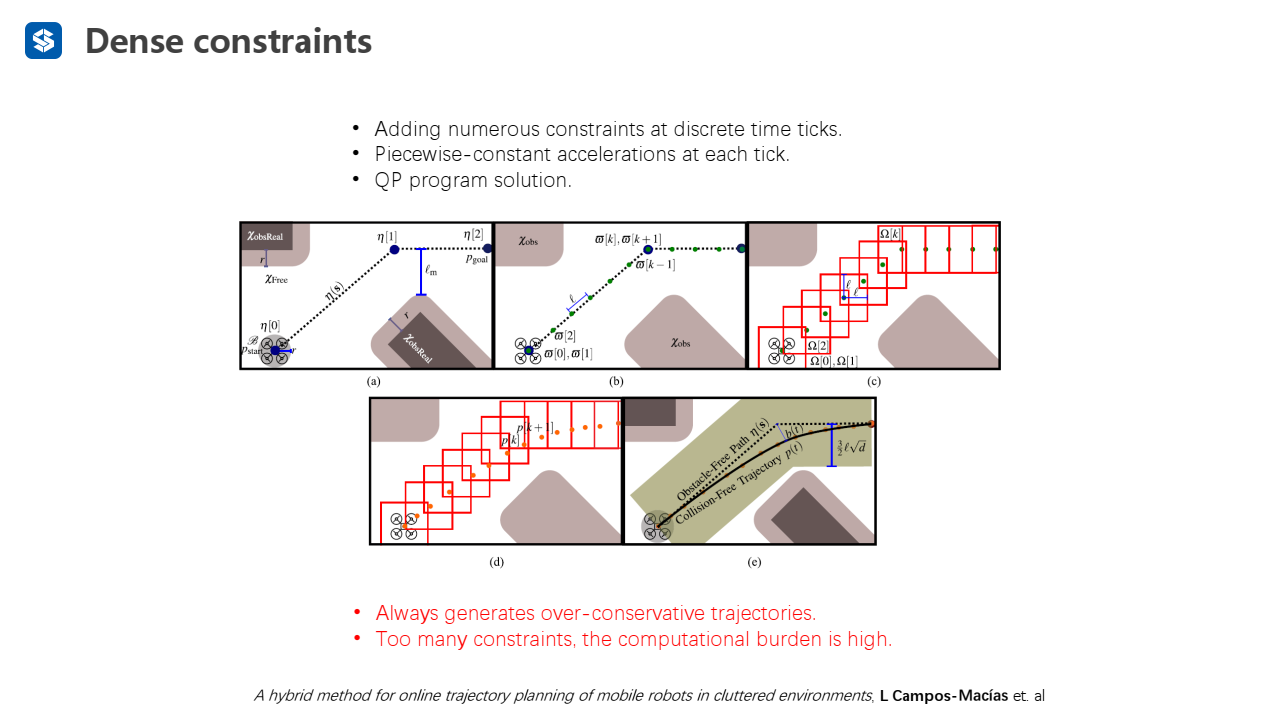
稠密地生成飞行走廊,在每段轨迹中加速度恒定(相当于用一个三次函数拟合),最后得到一组最优的(求解的变量少,一段轨迹只有一个)
但存在着生成的轨迹过于保守、太多限制条件导致计算负担较大的问题
Mixed integer optimization
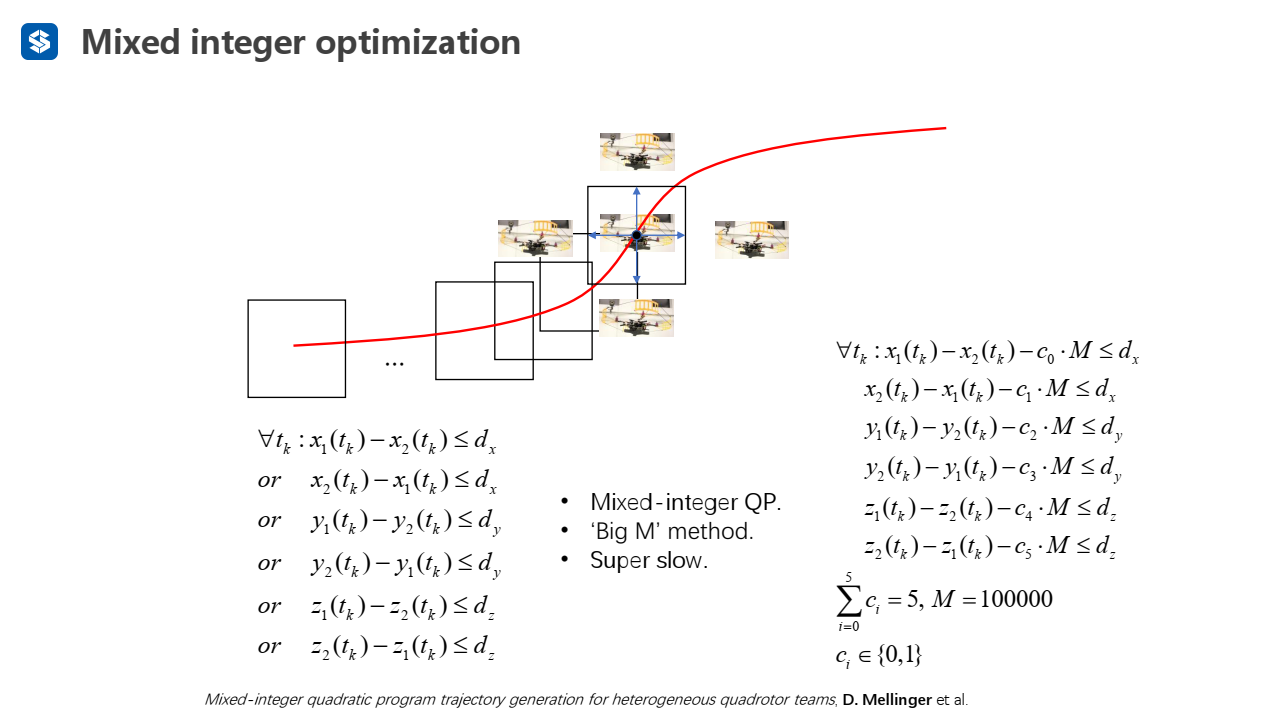
利用一个很大的整数M和一组选择整数将或运算转化为且运算
MIQP问题可以求解更快,但由于约束过多,导致求解较慢
软约束优化
基于距离的轨迹优化
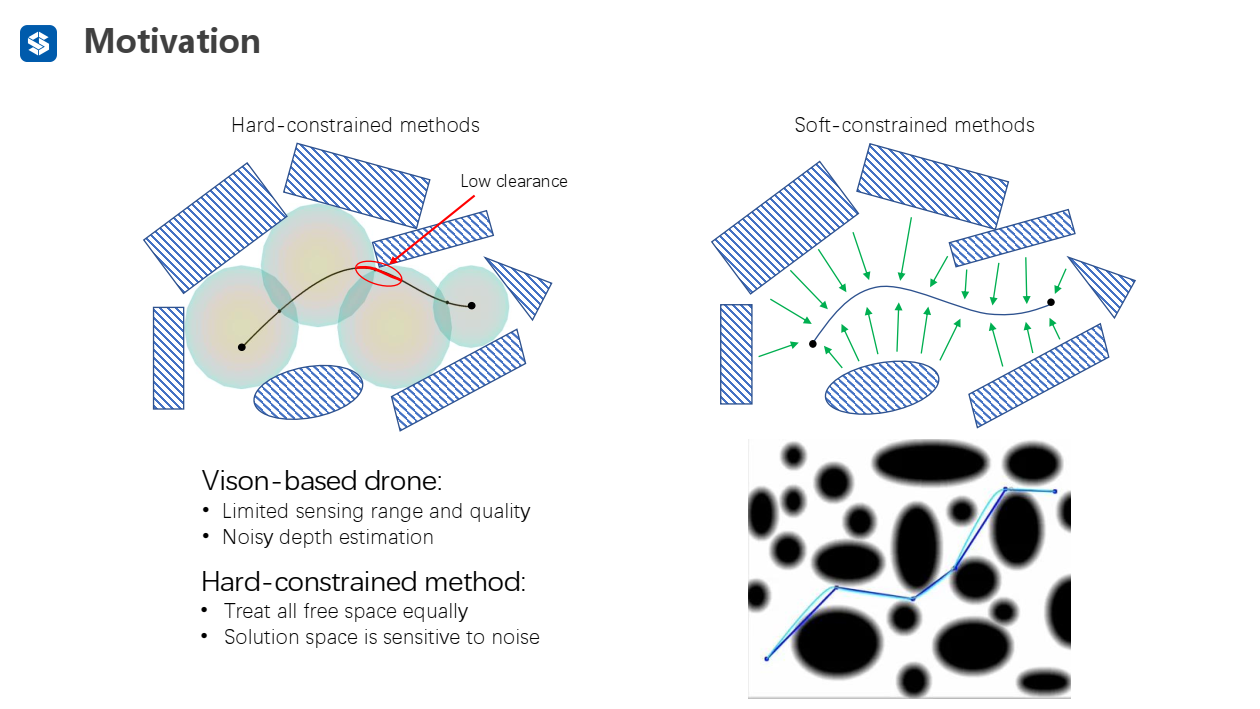
硬约束的轨迹优化存在的一些问题:
- 把安全区域当做等价的
- 解空间对噪声很敏感

光滑项闭式求解——相当于把约束直接加到表达式里了
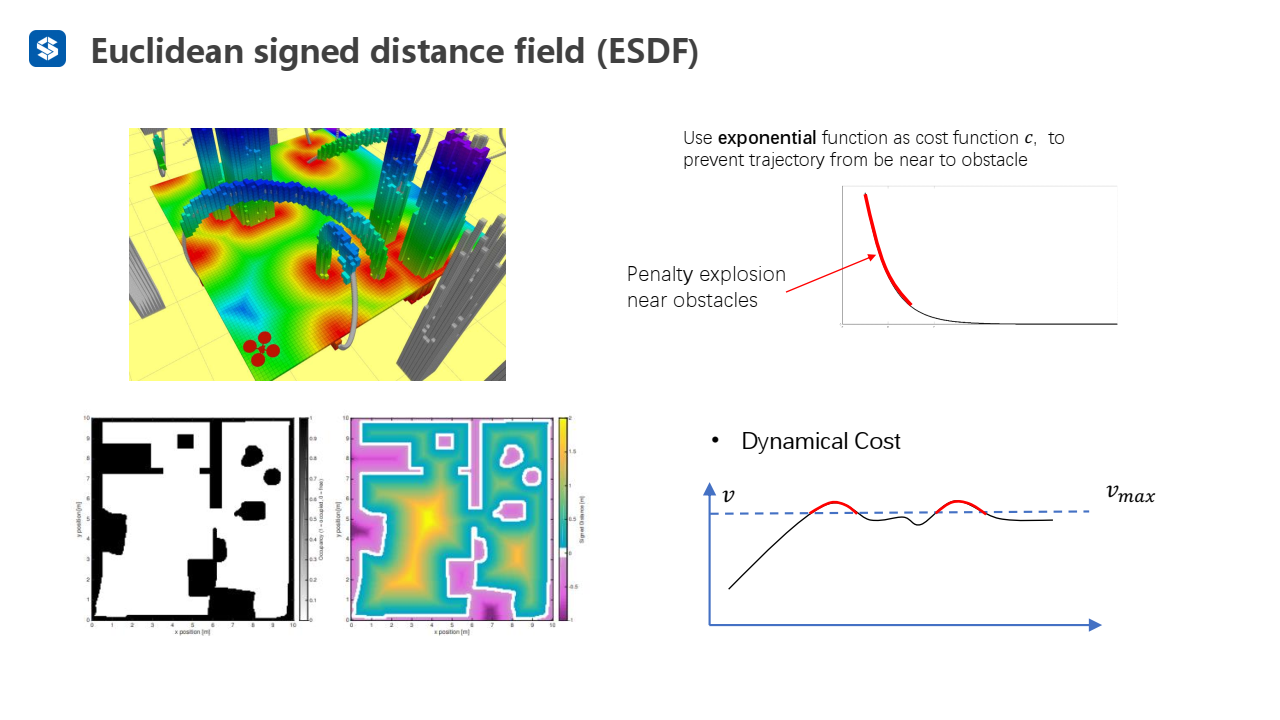
膨胀惩罚项——把轨迹上每个点在距离场中的碰撞惩罚()相加
碰撞惩罚项必须要把积分强行写成数值的解(要用轨迹上离散的点来评判碰撞惩罚)
动力学项:惩罚速度和加速度超过限制的部分

目标函数J不一定是凸的,因此不能将问题化为凸优化问题!只能用非线性优化的方法数值求解
利用链式法则求导
(可以用矩阵求导的方法得到结果)
()
数值优化



Line search的类型:
- exact line search——找到使函数下降到最低处的步长(实现较困难)
- backtracking line search——相当于给一个初始步长,然后判断在步长下是否满足(图中的表现就是在直线的下方,即),不满足则迭代缩小步长
梯度下降法
最速下降法

牛顿法


列文伯格—马夸尔特方法
详情可以看视觉SLAM十四讲
非线性优化库:Ceres(视觉SLAM用得比较多)、NLopt
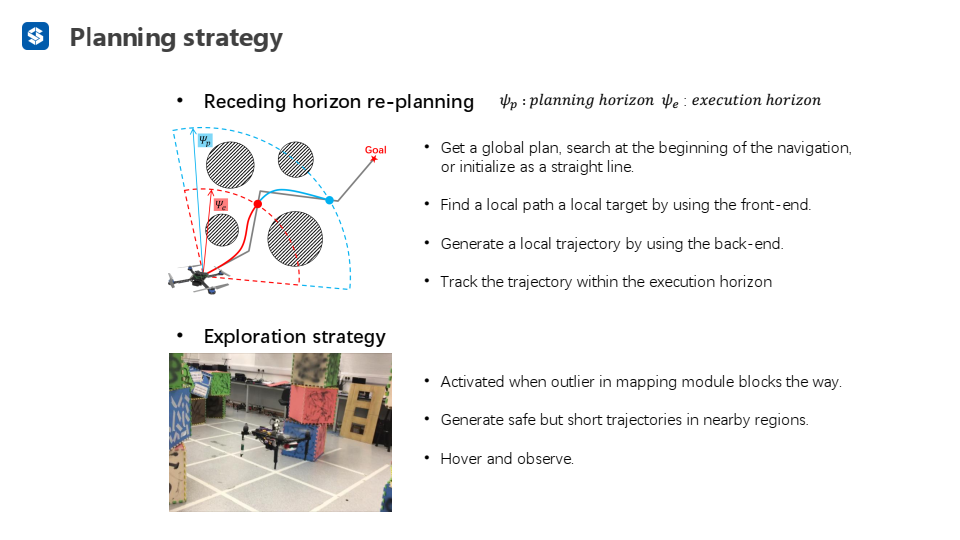
-
设置一个全局规划器(在导航一开始的时候,使用前端的路径规划搜索一条起点到终点的路径,作为全局规划器)
-
找到一个局部的路径
-
用后端生成一个局部轨迹
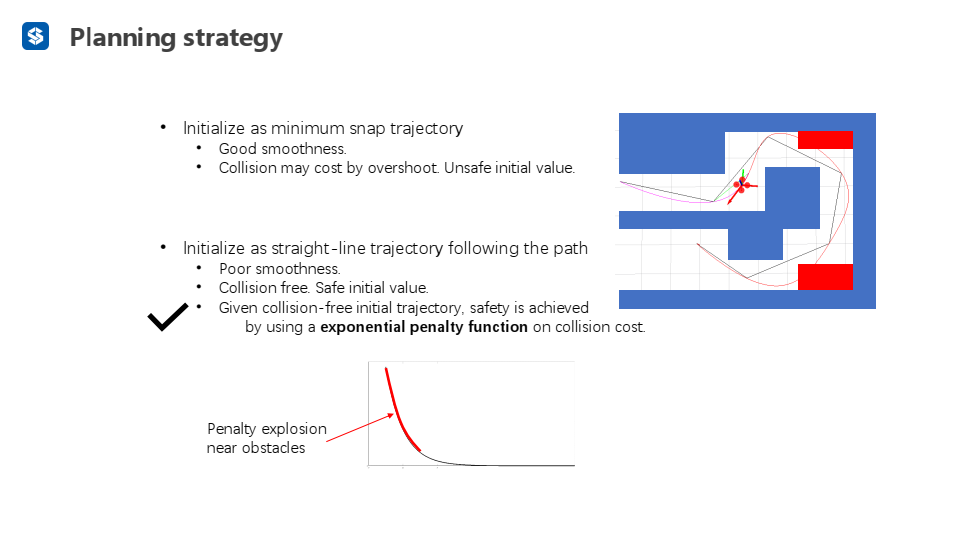
基于软约束的数值优化需要初值,可以选择minimum snap作为初值进行优化,生成的轨迹较平滑,但安全性较差;也可以选择直线轨迹作为初值,生成的轨迹平滑性较差,但安全性较好
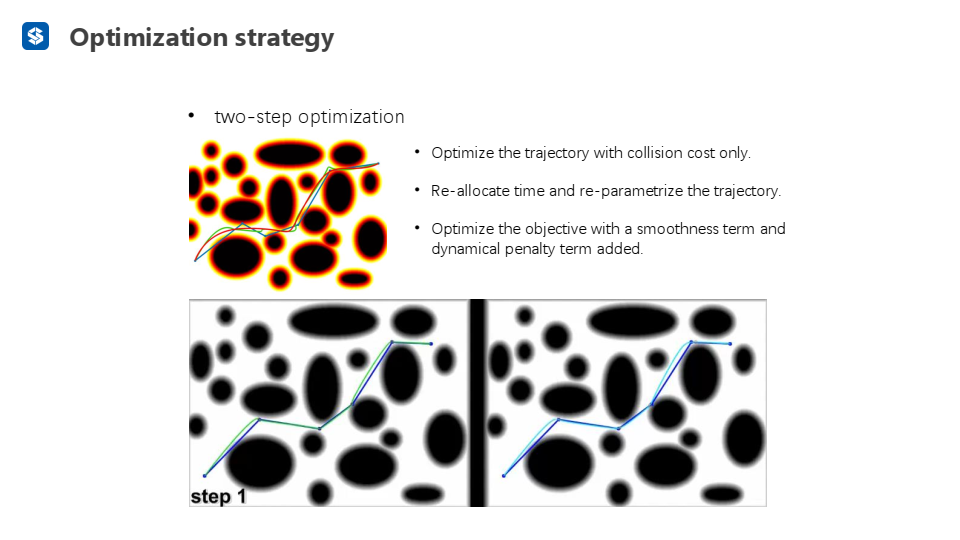
分两步优化:先只考虑collision cost进行优化,得到一条安全的轨迹;再添加smoothness term和dynamical penalty term进行优化,得到最终轨迹
Case Study
Fast Planner
Kinodynamic path searching + B-Spline trajectory optimization + time adjustment

算力负担较大,数值不稳定
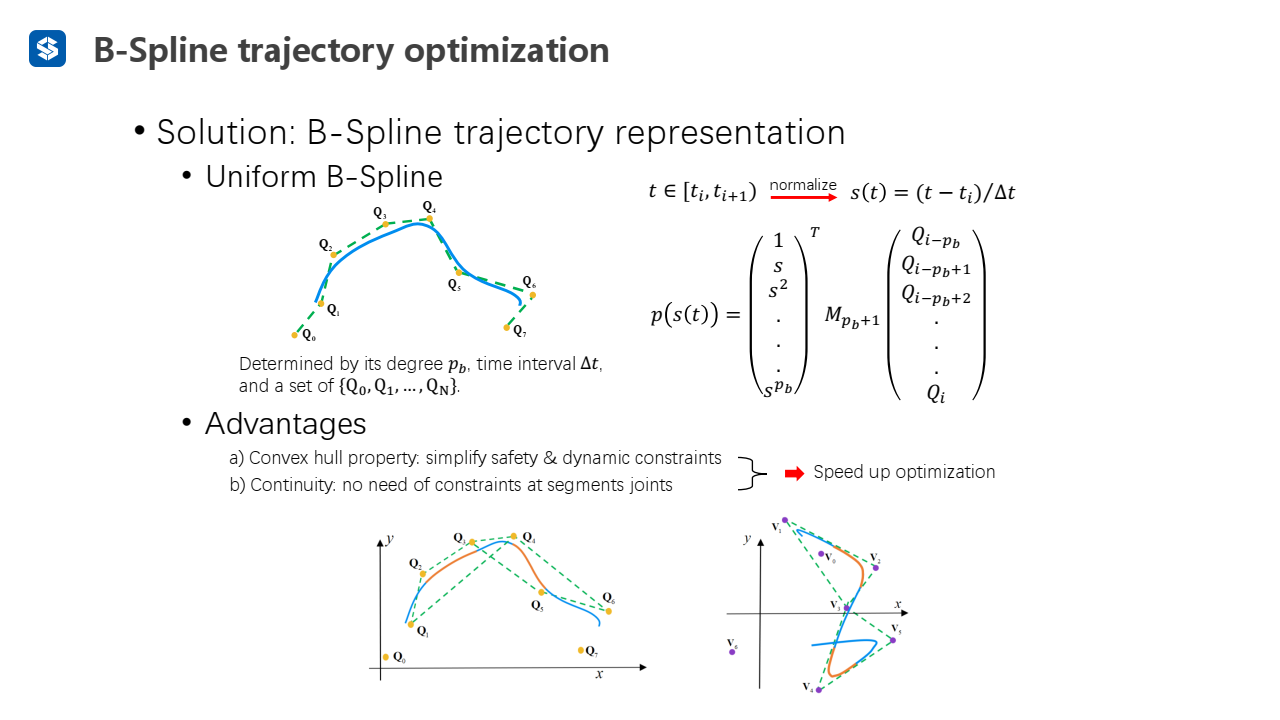
使用B样条曲线的优点:
- 曲线被包含在控制点组成的凸包内
- 曲线全局连续,不用像贝塞尔曲线或者普通多项式曲线,需要分段,并且保证两段之间连续光滑
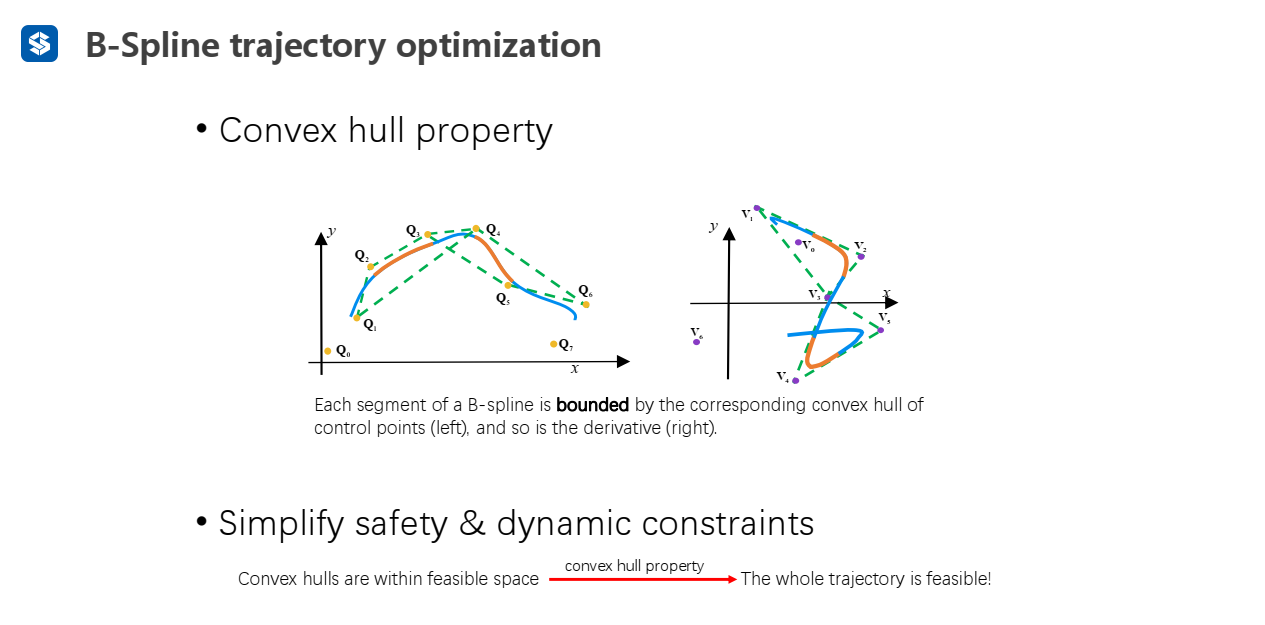
使用凸包性质可以将碰撞代价和动力学代价全部施加在控制点上
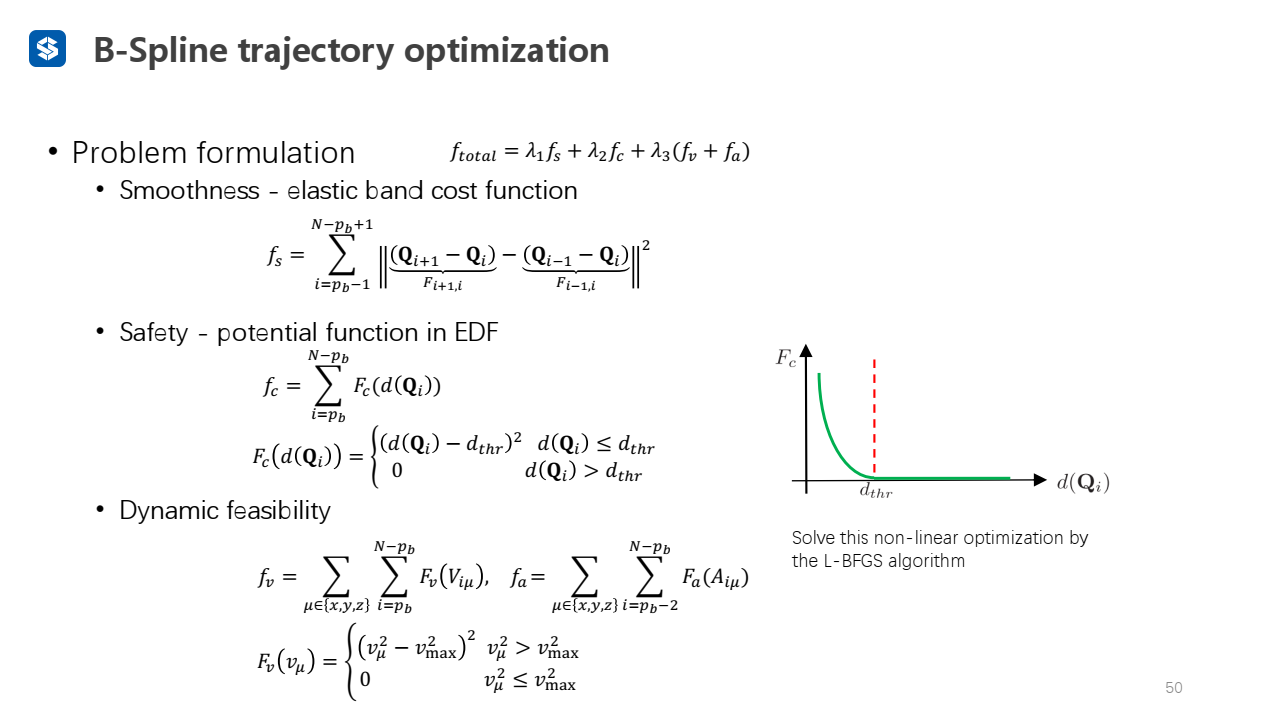
光滑项用——使用elastic band的代价函数
使用平方项作为碰撞代价和动力学代价,降低了算力的消耗,提高计算速度
