深蓝学院运动规划L5

基于Minimumsnap的轨迹优化

概述以及基础

轨迹优化的作用：提高解的质量

• Path quality
• Time efficiency

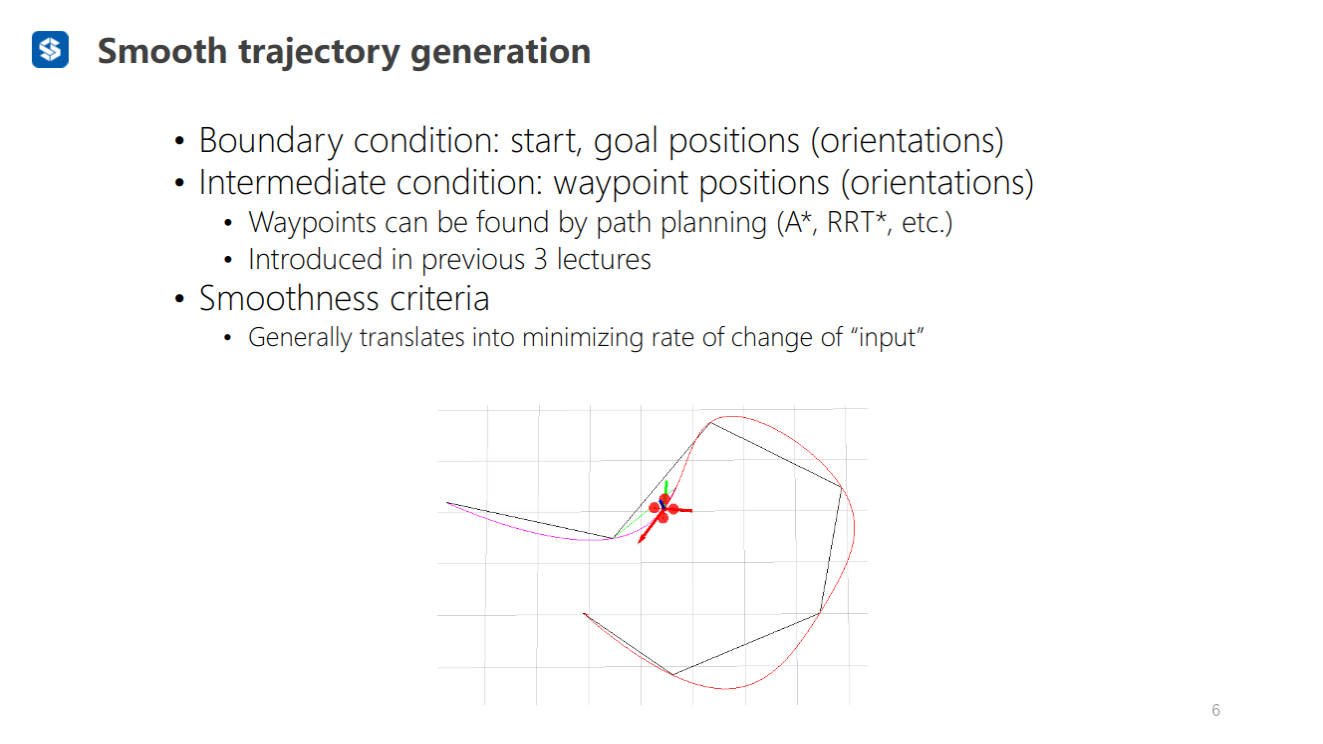
边界条件：起点、终点

中间条件：路点（前段路径规划生成的中间节点）

平滑准则

全维度的状态空间（$X$）里的路径规划问题可以转化为低维度的平坦的输出空间（$\sigma$）里的路径规划问题（要求：全维度的状态空间（$X$）可以被平坦的输出空间（$\sigma$）以代数组合的形式表示）

对于欠驱动的四旋翼来说，可以选择$\sigma=[x,y,z,\psi]^{\tau}$来作为平坦的输出空间（SE(3)：旋转加上位移、SO(2)：yaw方向上的旋转）

• 示例

  

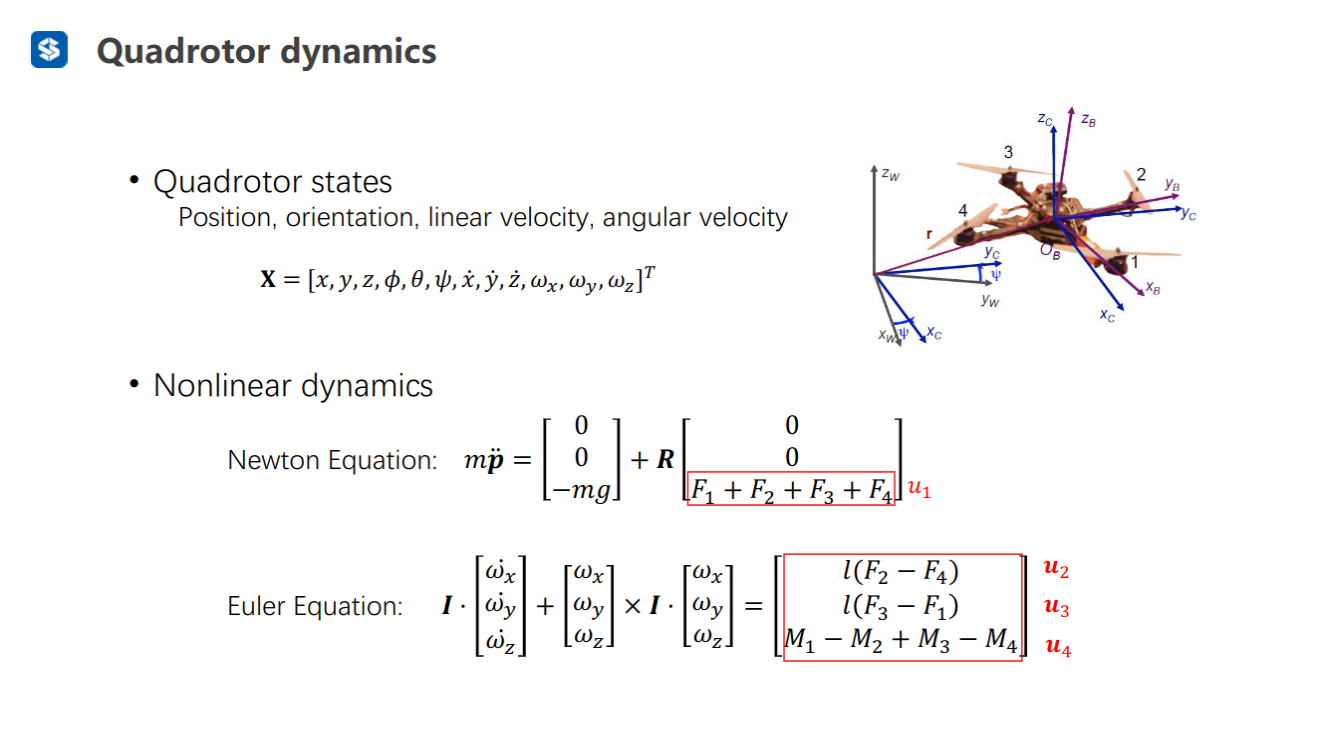
  四旋翼产生的推力的方向垂直于自身桨平面

  M1、M2、M3、M4是由四个螺旋桨旋转时所受的阻力矩产生的

  

  $Z_B$是利用前面所说的四旋翼的加速度方向垂直于桨平面来推导的（$Z_B$的方向为垂直于桨平面的方向）；$\sigma_1$表示$x$，$\sigma_2$表示$y$，$\sigma_3$表示$z$

  定义中间坐标系C（C和世界坐标系W差一个偏航角$\psi$），$Z_B$和$X_C$构成的平面垂直于$Y_B$（注意是Z-X-Y；$X_B$和$X_C$只差最后一次$Y_B$轴的转动，因此$Z_B$和$X_C$所在的平面垂直于$Y_B$）。故pitch、yaw、raw可以被$\sigma$空间表示

  

  

  知道$\omega_{BW}$后，先对其叉乘$z_B$，变成$h_{\omega}=-\omega_xy_B+\omega_yx_B$

  再对左右点乘$y_B$或者$x_B$，可以分离出$\omega_x$和$\omega_y$

  

  

  💡 主要需要注意的是四旋翼无人机是一个欠驱动的模型，桨片提供的推力方向和机身坐标系Z方向（$z_B$）相同，得到$z_B$在world中的表示

  又$z_B$在world中的表示=旋转矩阵$R$ * $z_B$在body坐标系中的表示（旋转矩阵$R=R(\psi)R(\phi)R(\theta)$，内旋ZXY（右乘）），可以利用R求解出$\phi$、$\theta$。故$\phi$、$\theta$可以被表示四个选定的量及其导数表示

  又$\dot {z_B}=\omega \times {z_B}$（已知$z_B$在world中的表示），故可以得到世界坐标系中四旋翼的旋转$\omega$。可以经过旋转矩阵将此$\omega$在四旋翼坐标系中表示（$^B\omega_B$—$\begin{pmatrix} \omega_{xB} \\ \omega_{yB} \\\omega_{zB} \\ \end{pmatrix}$—$\omega_{wb}$(body系绕world系的旋转)）

  💡 欧拉角的导数不能直接和$\omega_x$、$\omega_y$、$\omega_z$画等号，两者之间差一个矩阵！

凸优化

凸函数、凸集

任何凸问题的局部最优解是全局最优解

凸优化问题的标准形式

最小化、等式约束、不等式约束

$f_0(x),…,f_m(x)$均为凸函数，且等式约束左侧的函数为仿射变换（线性变换）的函数

线性优化（LP）、二次规划（QP）、有二次不等式约束的二次规划（QCQP）、二阶锥优化问题（SOCP）（可以包含LP、QP、QCQP）

半正定优化问题

Minimumsnap

Minimumsnap的阐述

使用多项式函数的好处：

• 多项式阶数可以保证平滑性准则
• 推导计算方便
• 可以把三维的轨迹生成解耦

一维的多段平滑轨迹（考虑初末速度）

每一段的初末速度由求解优化问题指定更为合理（引入Minimumsnap）

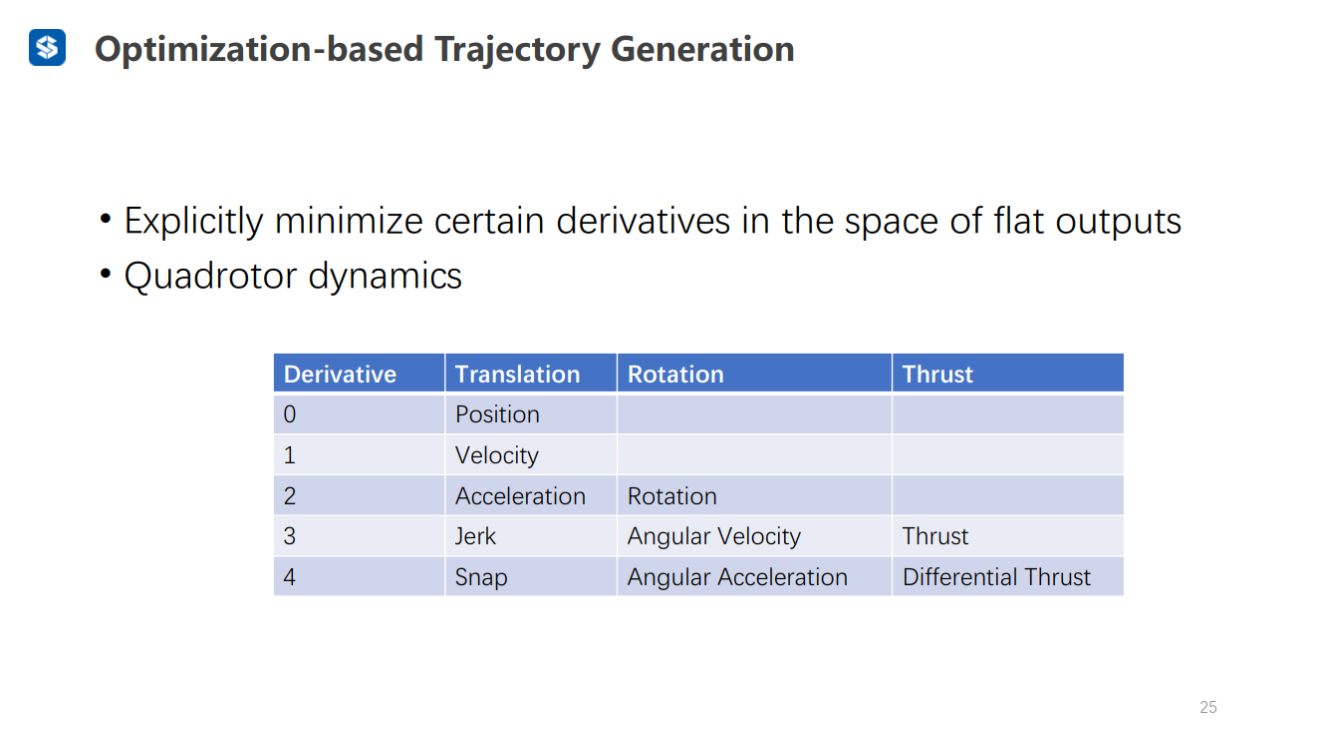
Minimum jerk：最小化角速度，利于视觉跟踪

Minimum snap：最小化推力变化，节省能量

每一段轨迹阶数不一定相同，阶数相同可以简化

每段时间必须已知——时间分配

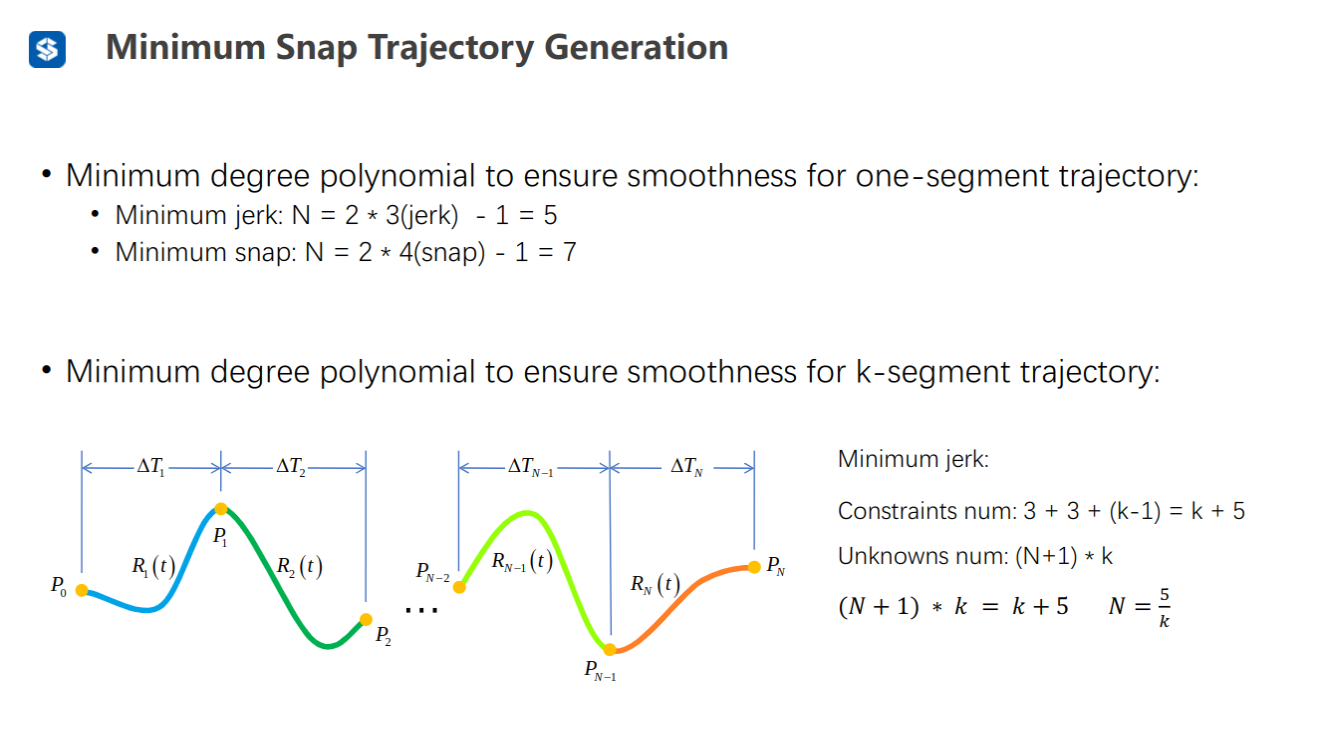
一般认为，对于单段的轨迹来说，最小化jerk要保证首末p、v、a已知，共有6个约束，故多项式至少为5阶（要解最优化问题——保证自由度≥约束数，否则没有意义）

对于k段的轨迹来说，最小化jerk要求保证首末p、v、a已知，以及中间的k-1个位置约束

💡 这里推导k段轨迹的多项式最低次数时，只考虑了首末端点p、v、a约束和中间路点的位置约束（3+3+k-1），有点问题

推导时还应该考虑中间路点p、v、a连续性约束（3*(k-1)），因此等式为

$(N+1)*k=6+4*(k-1)$ $N=3+{2 \over k}$

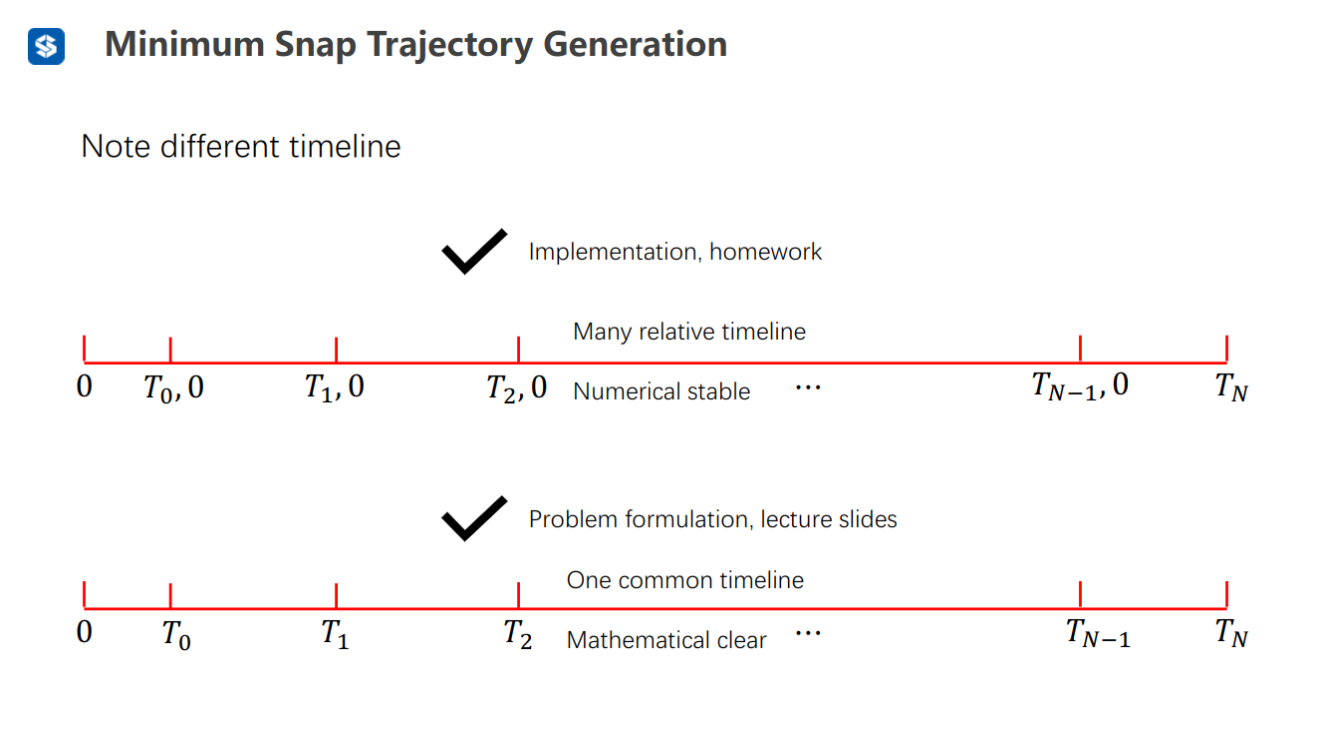
时间线用相对时间线更好，每一段时间都从0开始，数值上更加稳定

Minimumsnap的求解

最小化J值

二次型矩阵

整个轨迹上的目标函数形如$J=\begin{vmatrix}Q_1 & 0 &0\\ 0 & Q_2&0\\0&0&Q_3 \end{vmatrix}$ ，也是一个二次型矩阵

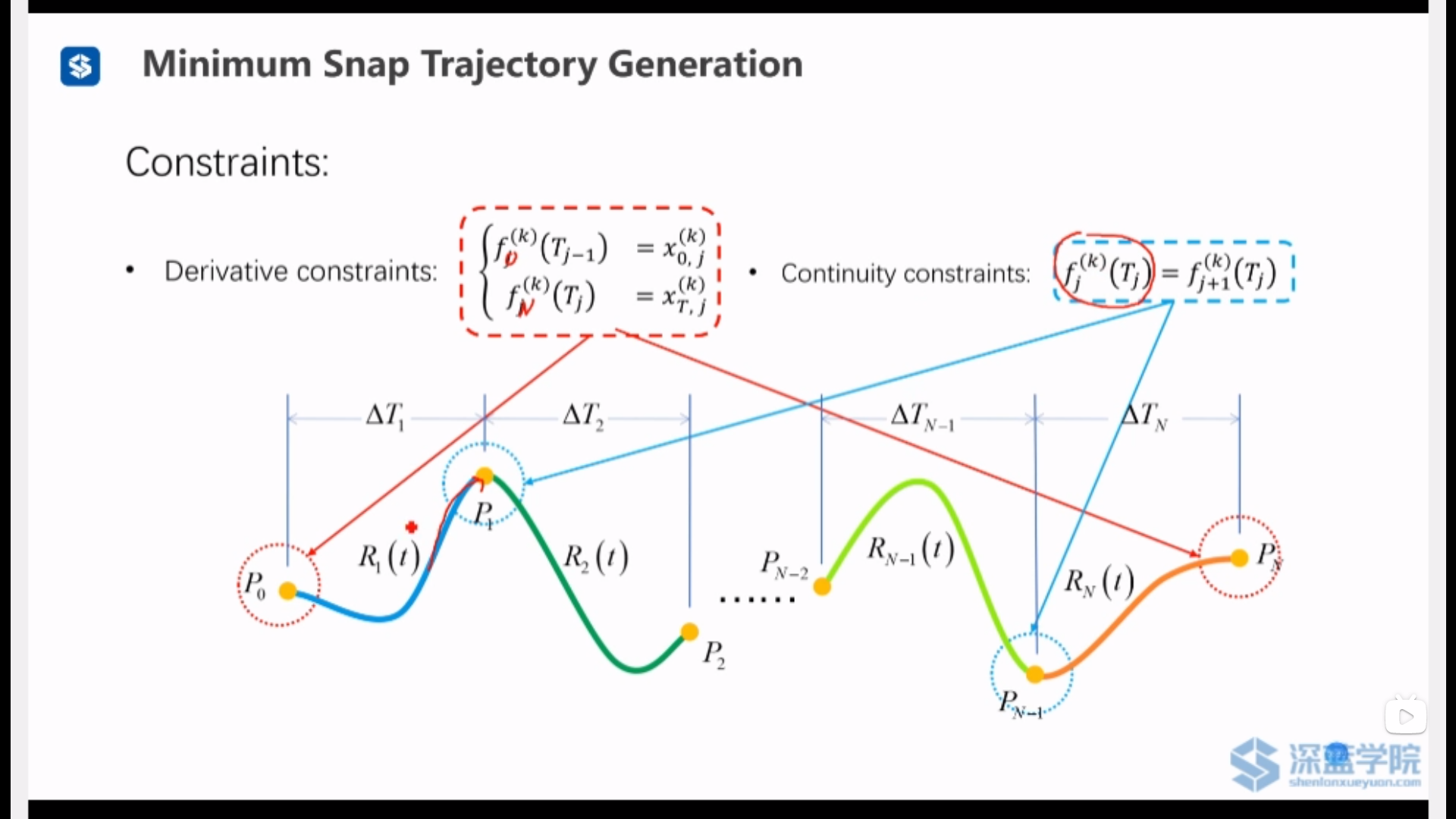
导数约束（首末两点的p、v、a、j，以及中间节点的p约束）

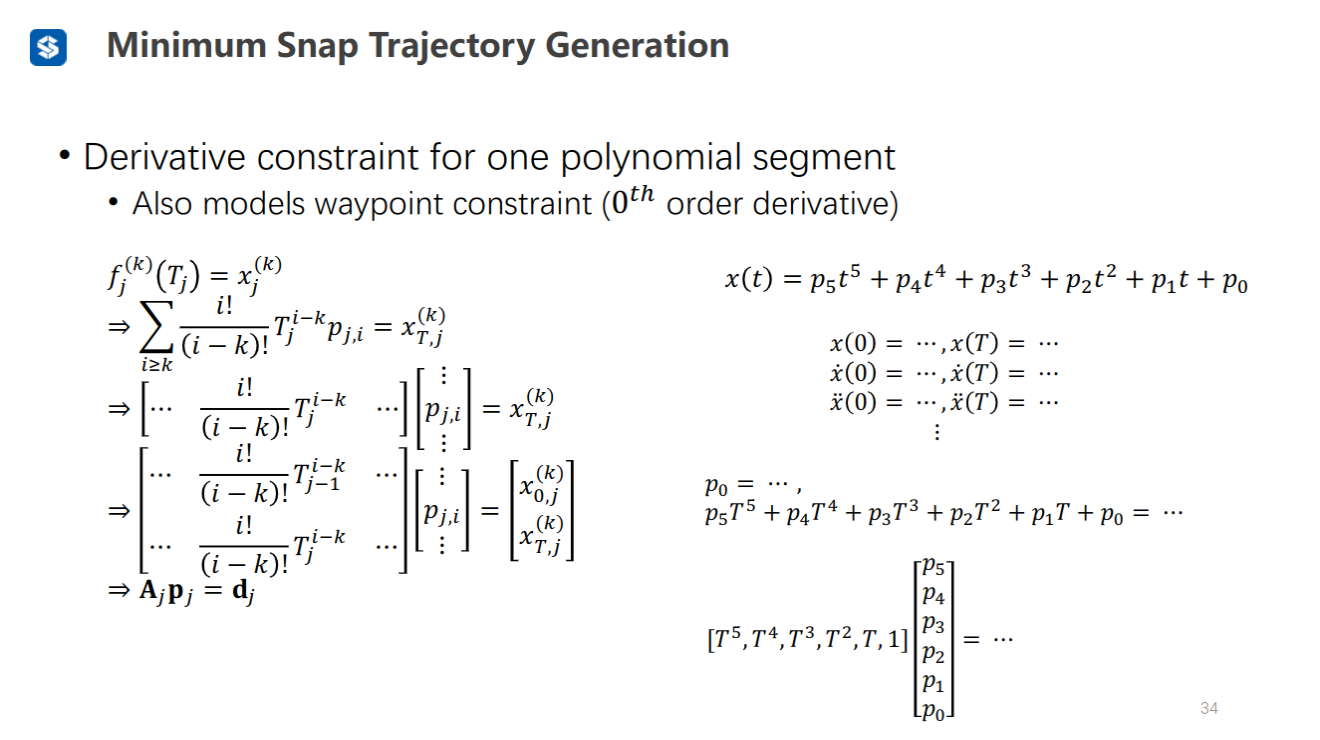
只跟当前段有关

连续性约束

跟前一段和当前段有关

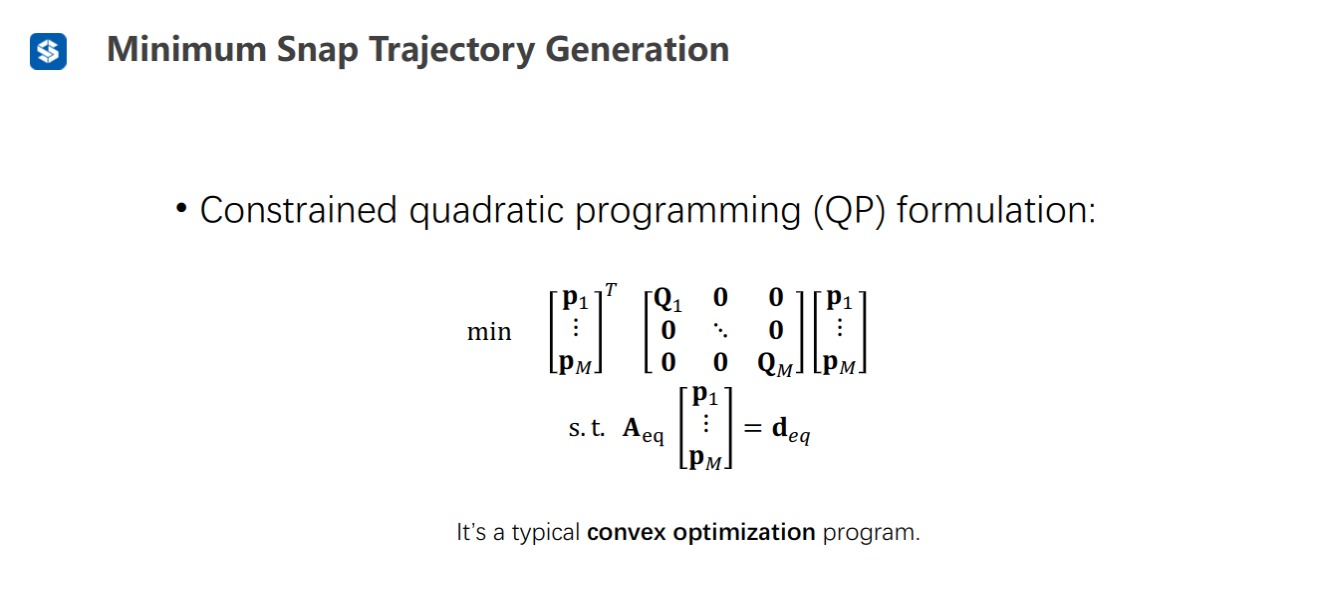
导数约束和连续性约束可以化成一个大矩阵

二次优化问题——QP问题（典型的凸优化问题）

转化成凸优化问题后可以用凸优化求解器求出数值解

把多项式系数转化为各阶导数

直接优化多项式轨迹容易数值不稳定（比如T很大时，高阶项系数往往很小）

利用映射矩阵M，将多项式系数转化为导数（v、a），而这些导数理论上是数值稳定的（正常机器人运动时v、a并不会太大）

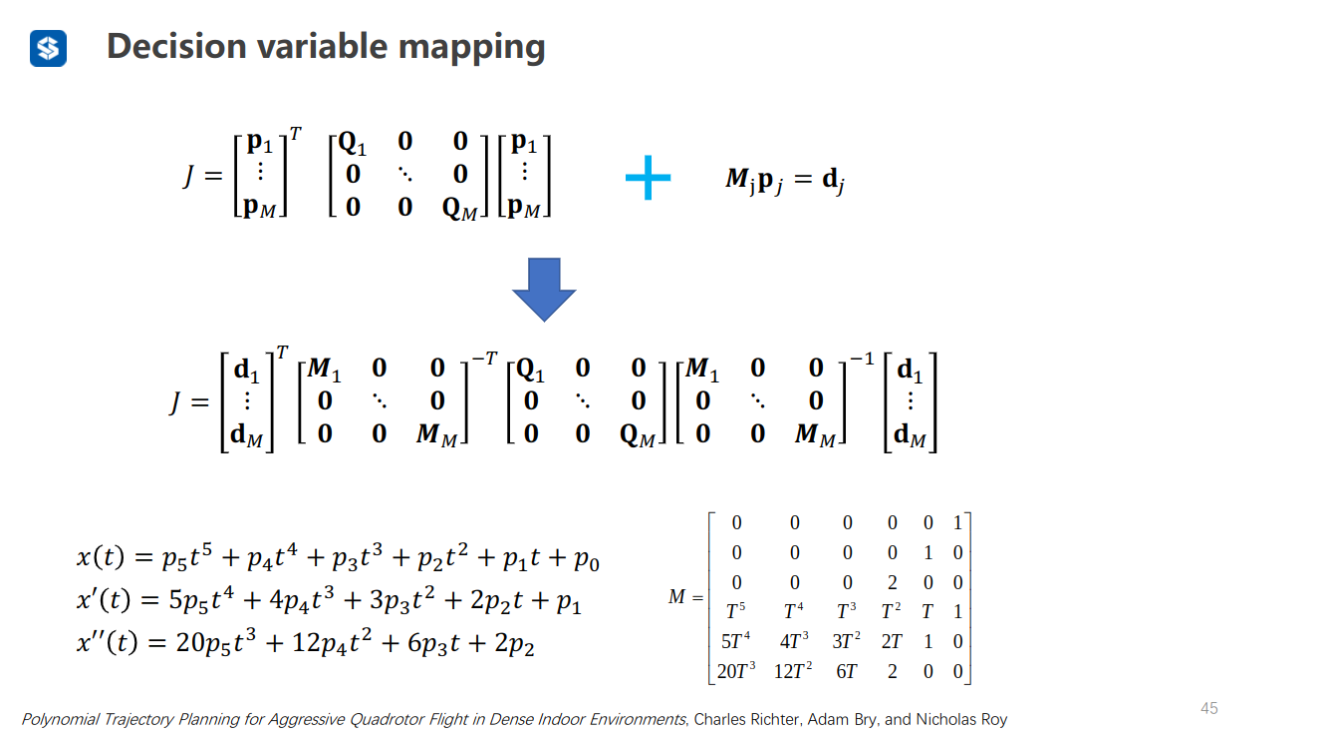
分离固定和自由变量（要优化的变量相当于中间节点的v、a）

利用选择矩阵C，分离出受约束的导数（$d_F$）和需要被优化的导数（$d_P$）

$d_F$相当于已经添加了导数约束，而连续性约束可以通过选择矩阵来进行保证$d_{N-1}$的末尾时刻等于$d_N$的初始时刻

将带约束条件的优化问题转为不带约束条件的优化问题（对$d_P$求偏导，利用导数等于0）

💡 求导方法如下：

矩阵求导术

PS：R为对称矩阵（$R=R^T$），故$R_{FP}=R_{PF}^T$

构造$C^T$——闭式求解Minimumsnap的关键

Others

安全性问题：轨迹优化后可能超调，与障碍物发生碰撞

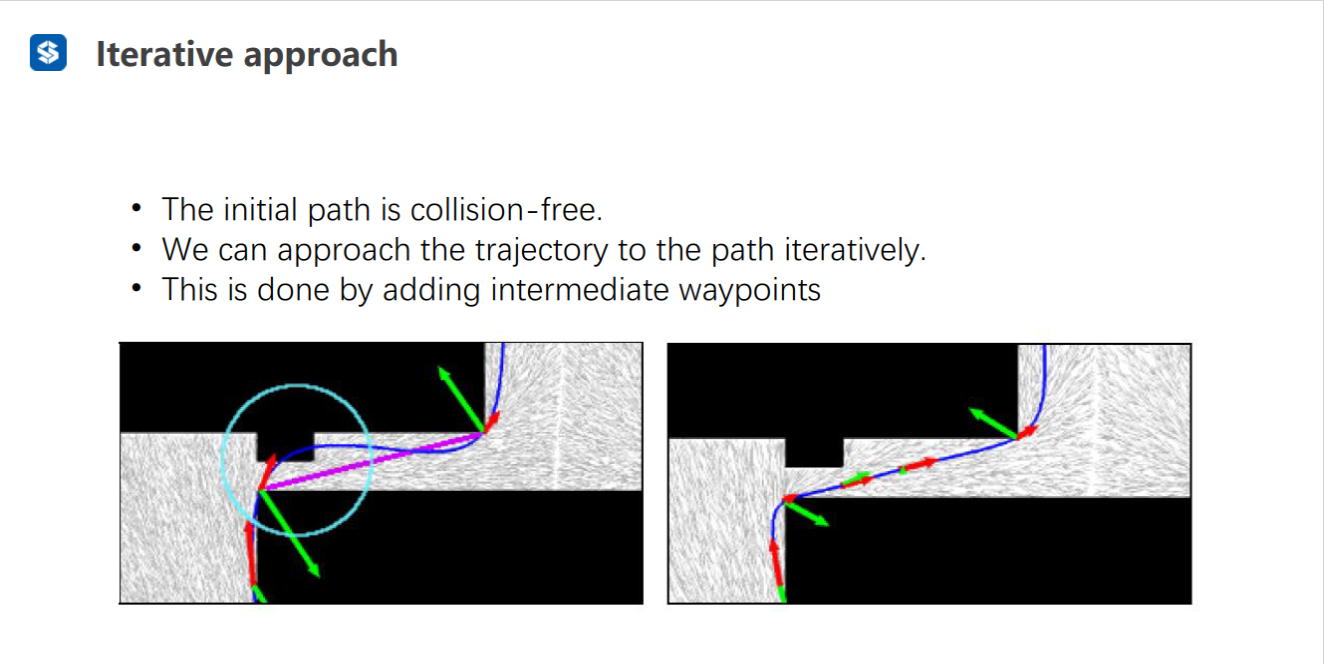
轨迹和障碍物发生碰撞时，可以在中点处添加一个新的路点，对碰撞端的轨迹进行局部的重新生成。重复这一步骤，直至不会发生障碍物的碰撞

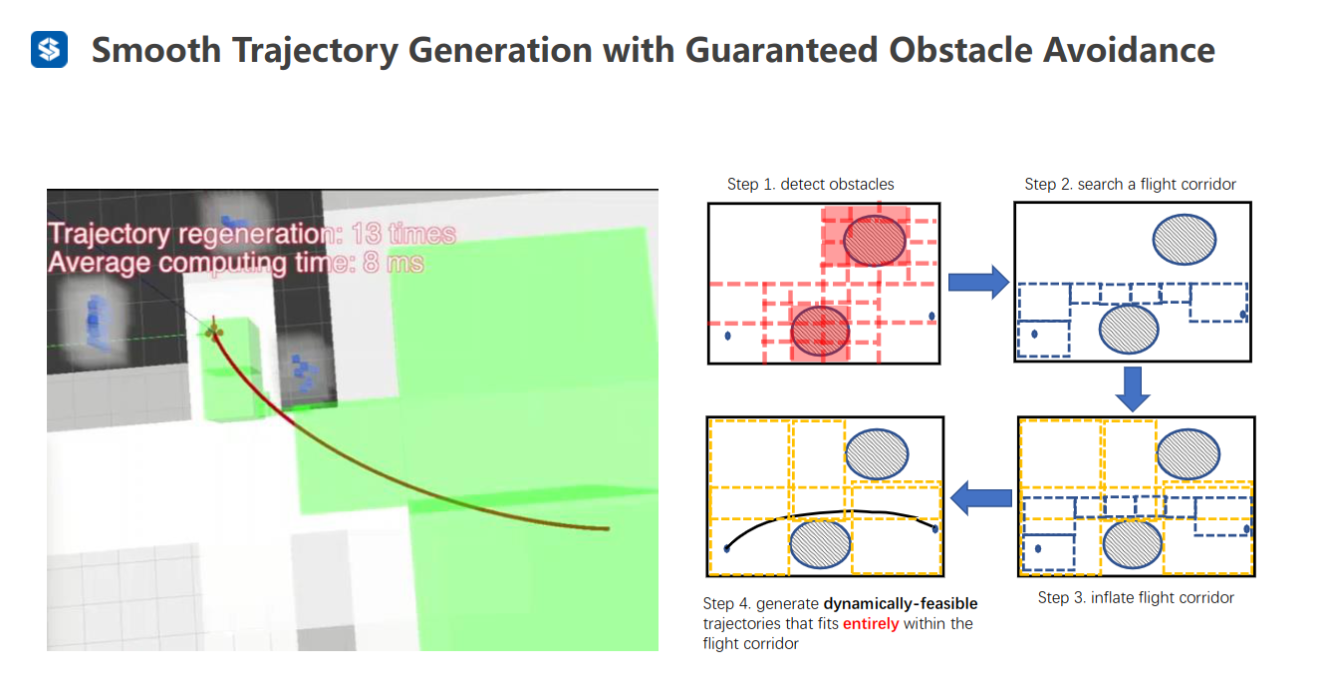
利用bounding box施加约束（每段轨迹必须在bounding box里）

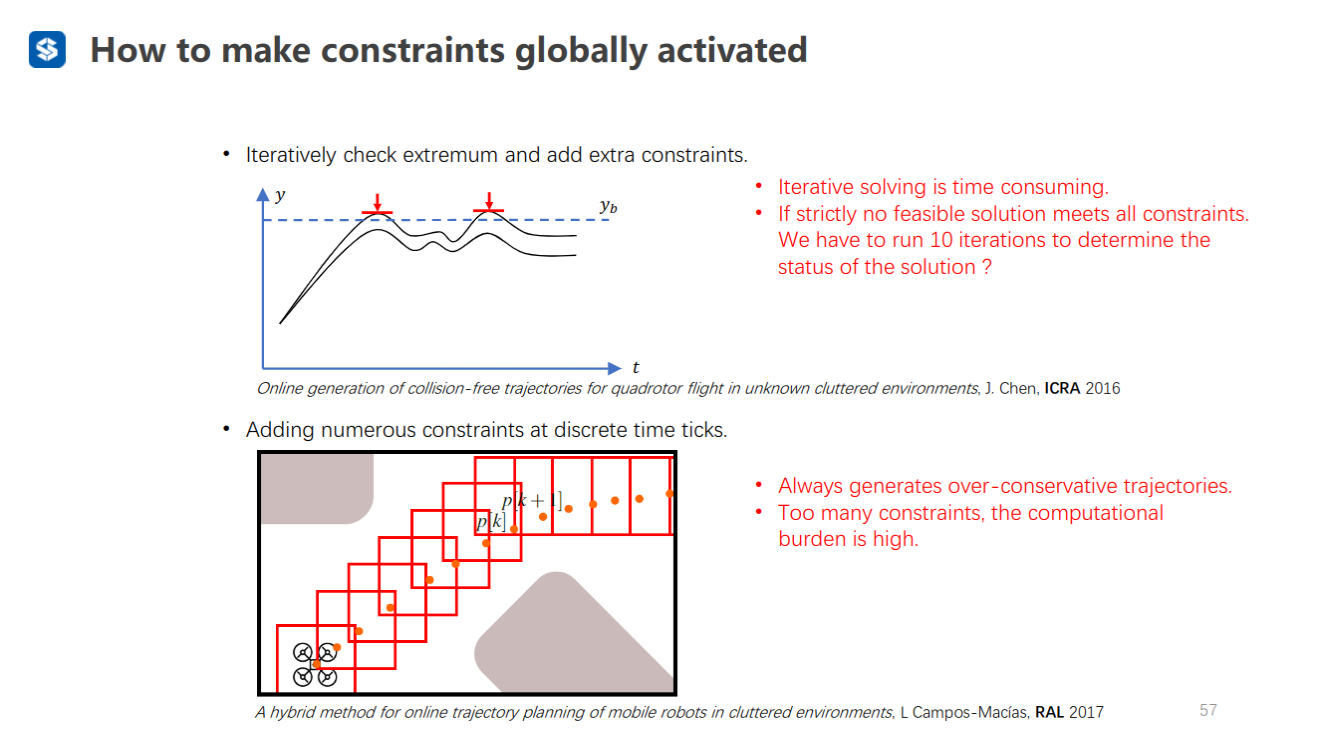
保证轨迹在bounding box的解决方案

• 迭代地求解轨迹的极值（如果超过bounding box，施加额外的约束，继续求解）
• 密集生成bounding box

一些凸优化求解器：CVX（Matlab wrapper）、Mosek（好用，但只能在x86架构运行——官方只给了x86的library）、OOQP（求解QP问题很快，代码开源）、GLPK（求解LP问题）、OSQP

数值稳定性问题

• 时间稳定性
  • 使用相对时间轴（可以解决多段路径累计时间开销长，导致的数值不稳定的问题）
  • 将时间轴进行放缩，每一段的时间归一化（1.0）（可以解决单段时间开销和很小或很大，导致的数值不稳定的问题）
• 空间稳定性
  • 如果是大规模场景，空间开销较大，导致数值不稳定的问题，可以对空间进行归一化——等比例缩小成一个场景，求解小场景中的问题

问题1：一般情况下，独立的求解三个单轴的优化问题比直接求解一个三轴的优化问题的效果好；但在软约束的条件下，最小化的量包含距离信息（$\sqrt{x^2+y^2+z^2}$），x、y、z三个轴不能单独优化，只能选择直接求解一个三轴的优化问题

问题2：闭式求解一般来说比直接数值求解更稳定，但当矩阵大的时候闭式求解可能会导致不稳定；而数值求解可以引入工程性操作来保证稳定性

问题3：最小化某一阶的平方时，多项式是问题的最优解；但在其他情况下，多项式可能只是最优解的一个子集

时间分配

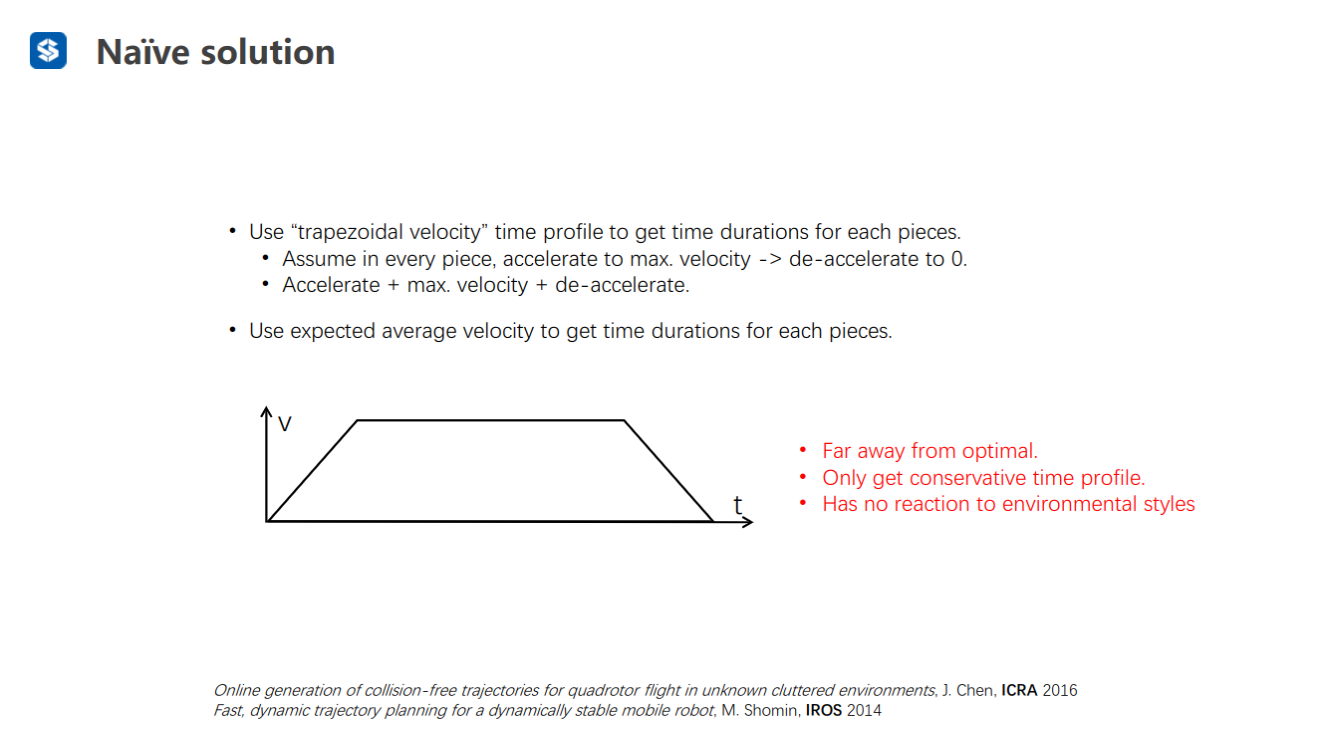
每一段时间分配都是梯形规划，得到的时间较保守

bounding box提供了一个解空间的自由度，中间节点可以在两个bounding box交界处自由移动，一定程度上可以缓解时间分配不好导致的问题

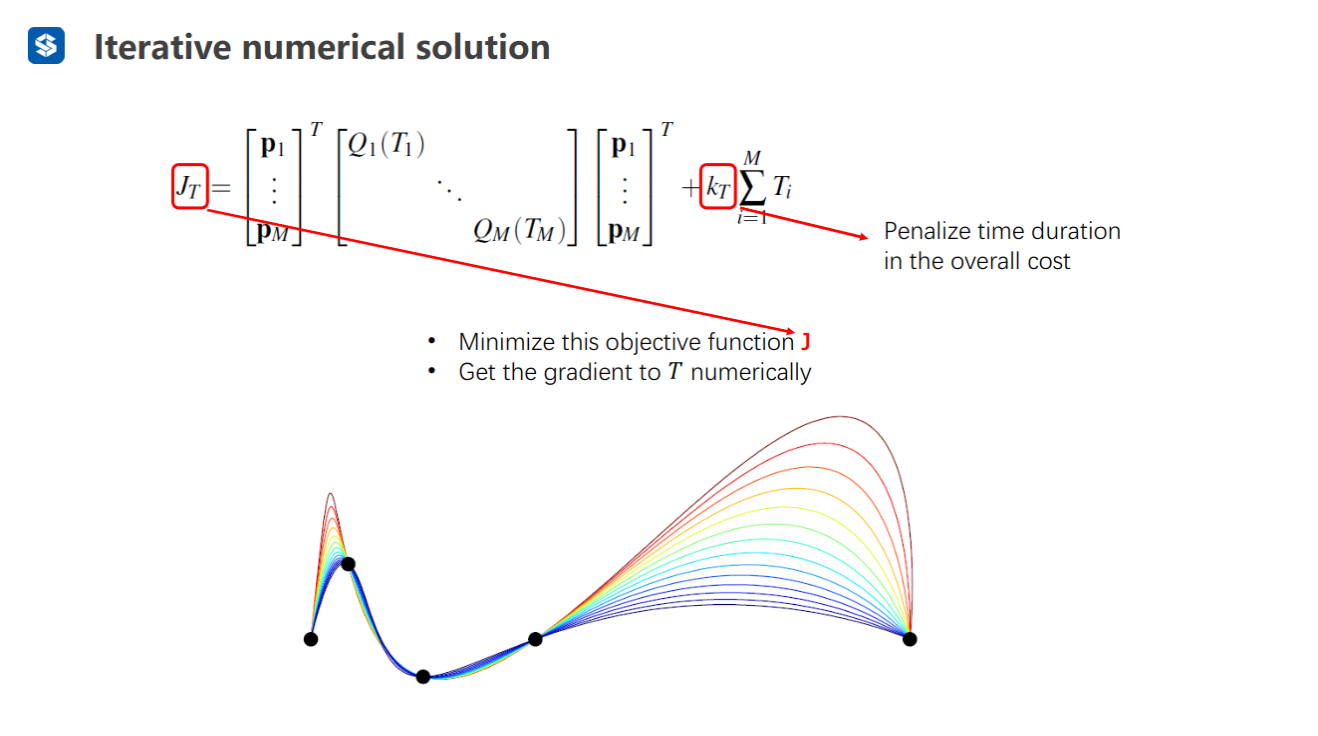
最小化的值加上时间的权重：无法解析式求解、只能数值求解——不断迭代（梯度下降法）

如果优化出的时间不满足动力学可行性——则可以延长总时间，但保证各段时间之间的比例

💡 Minimum snap为什么不能像OBVP优化时间？

OBVP可以将J表示成时间的函数，对时间求导，从而最优化时间；

而Minimum snap构造出的QP问题闭式求解时（解析解），得到目标函数$J=d_F^TR_{FF}d_F+d_F^TR_{FP}d_P+d_P^TR_{PF}d_F+d_P^TR_{PP}d_P$，当时间T已知时，R项为常数，才能对$d_P$求导。当时间T未知时，R项为泛函，$d_P$也为泛函，不能分析问题。