满足动力学约束的路径规划
概述

满足运动学约束(Kinematic)和动力学约束(Dynamic)
约束一般要考虑到力的层级(加速度)
机器人有一定的动力学模型,不能当成质点来处理,考虑机器人高阶的约束
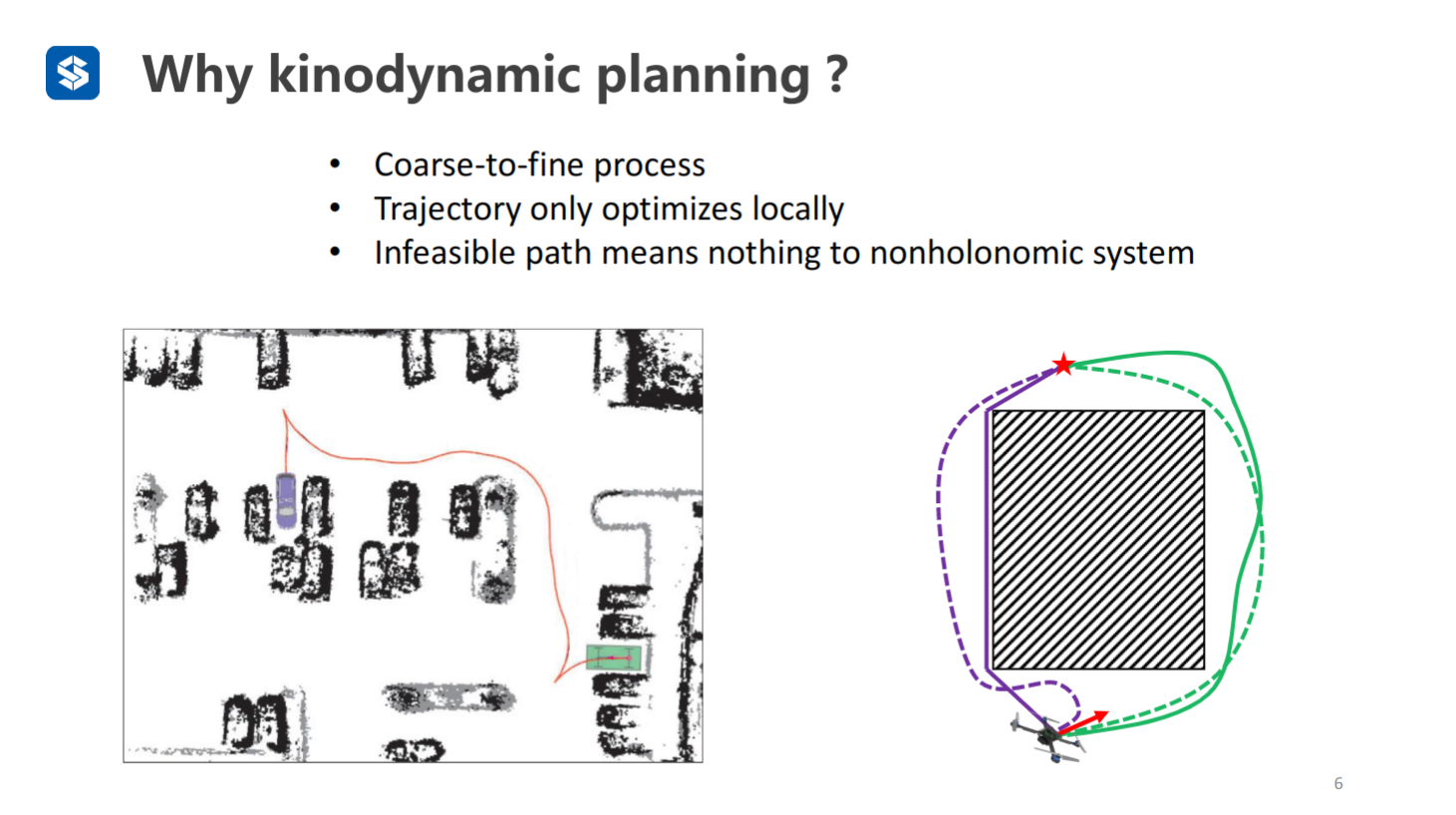
- 从粗到细的优化过程
- 轨迹只需要局部优化

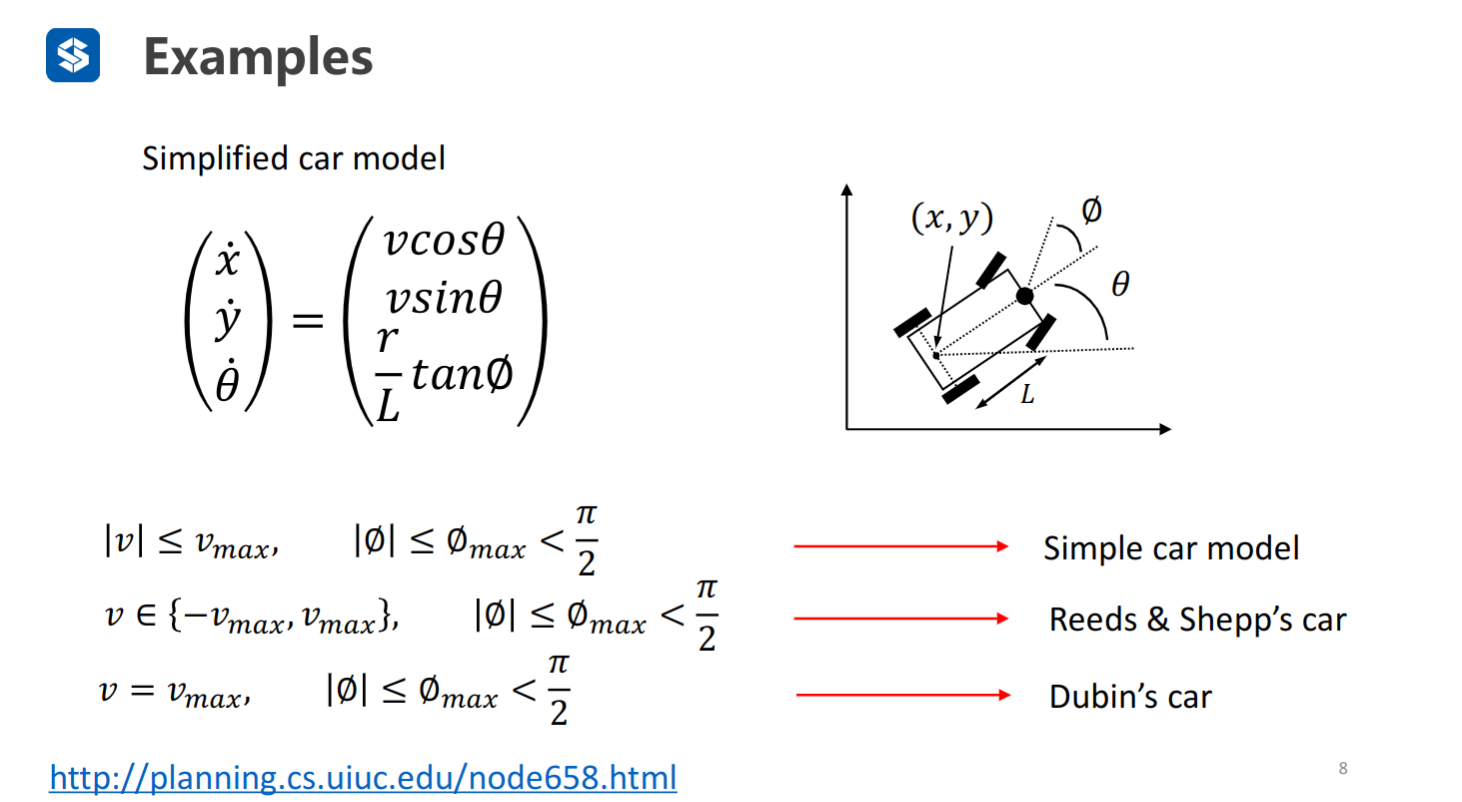
该模型前轮负责转向,后轮负责驱动
上述公式角速度计算公式有误——应为
一些经典的动力学模型
状态栅格搜索算法(State Lattice Planning)
搜索算法的核心是如何根据使用场景来构建一颗搜索树:
- A*和PRM等算法就是先构建好搜索图,再构建搜索树
- RRT是一边构建搜索树,一边拓展节点
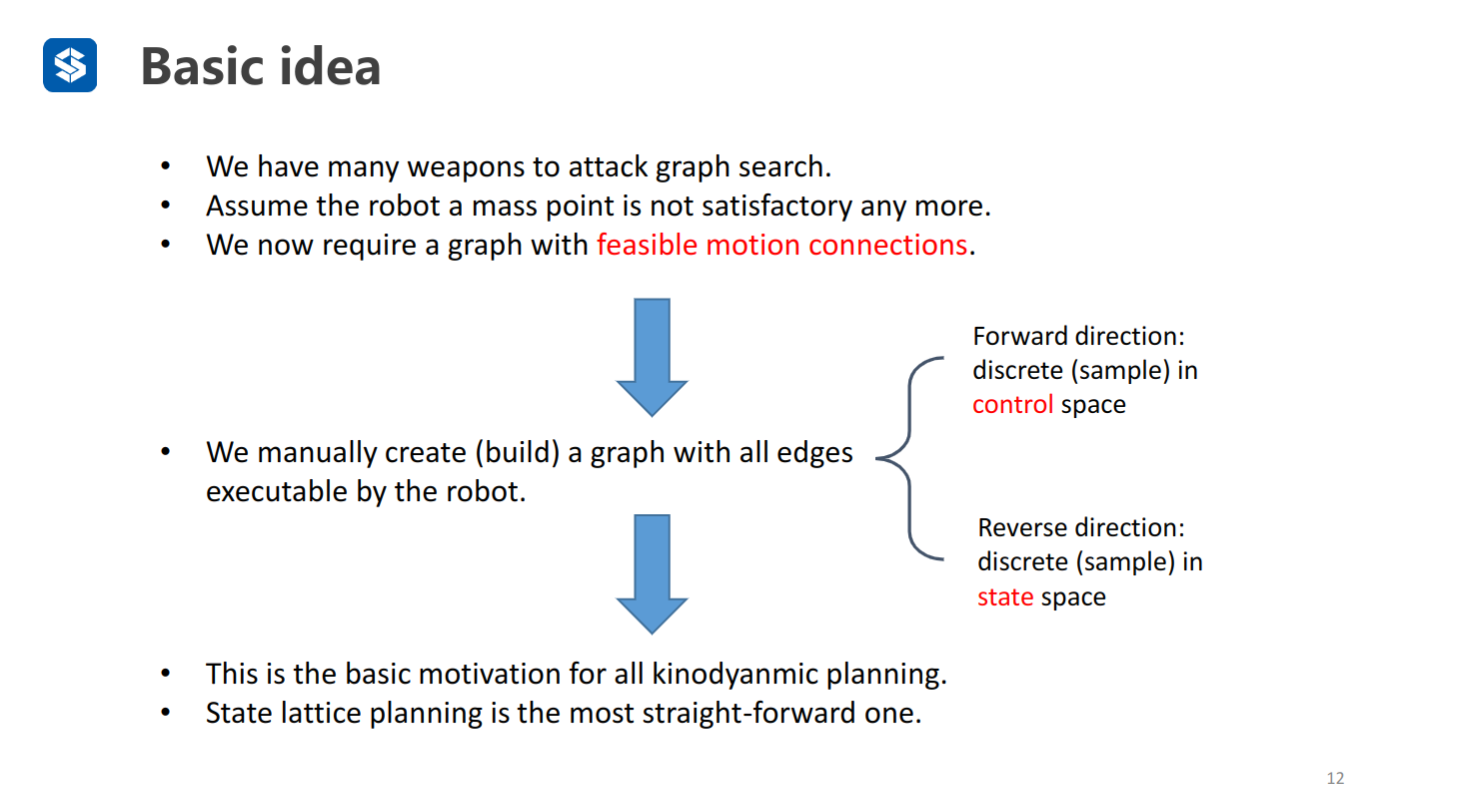
建立一个所有边可以被机器人执行的图:
-
正向:离散机器人的控制空间(驱动机器人向前运动,得到多个feasible motion connection)
-
逆向:离散机器人的状态空间(在机器人的状态空间里产生多个点,寻找连接)
-
示例
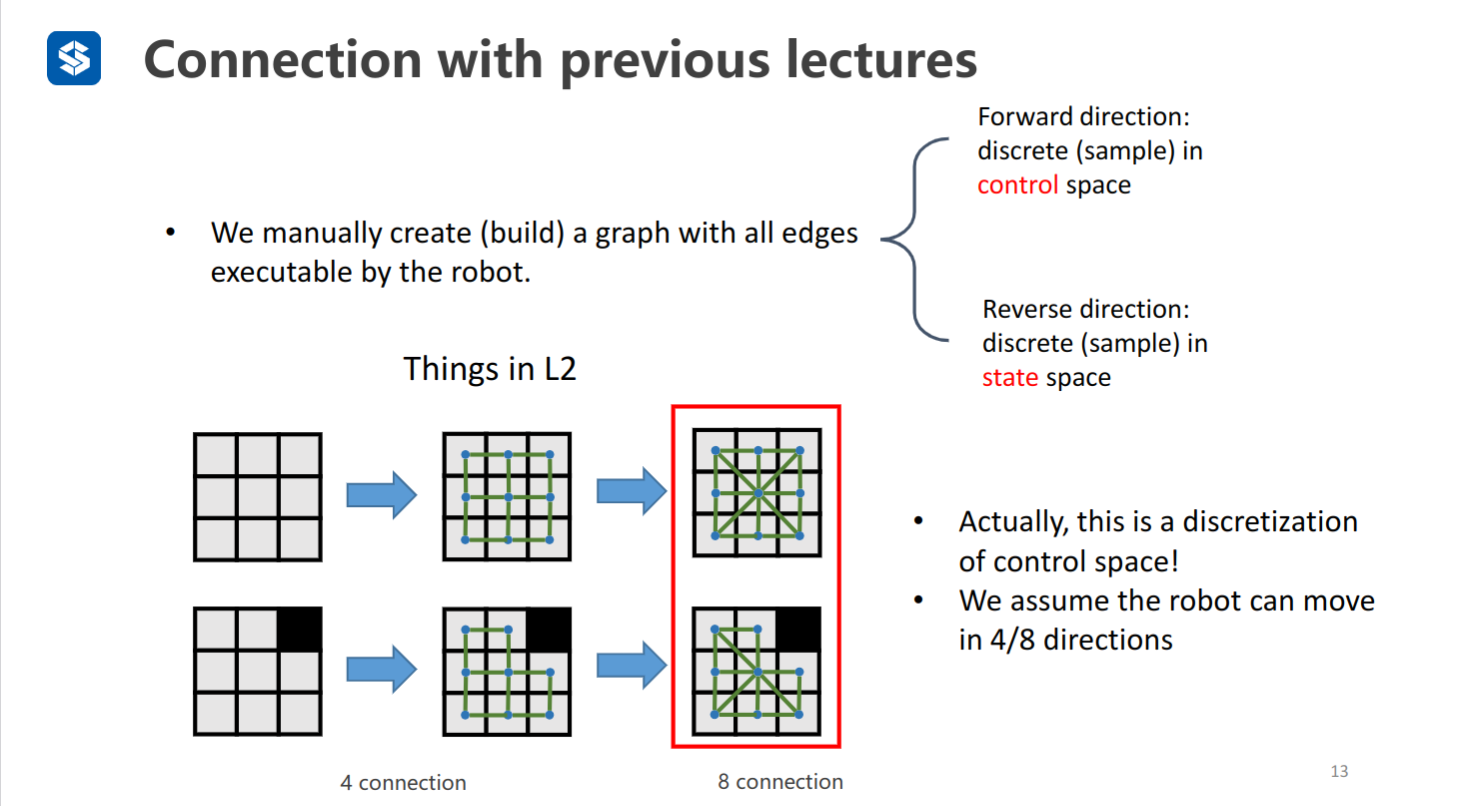
四连接和八连接图就可以看做离散了机器人的控制空间
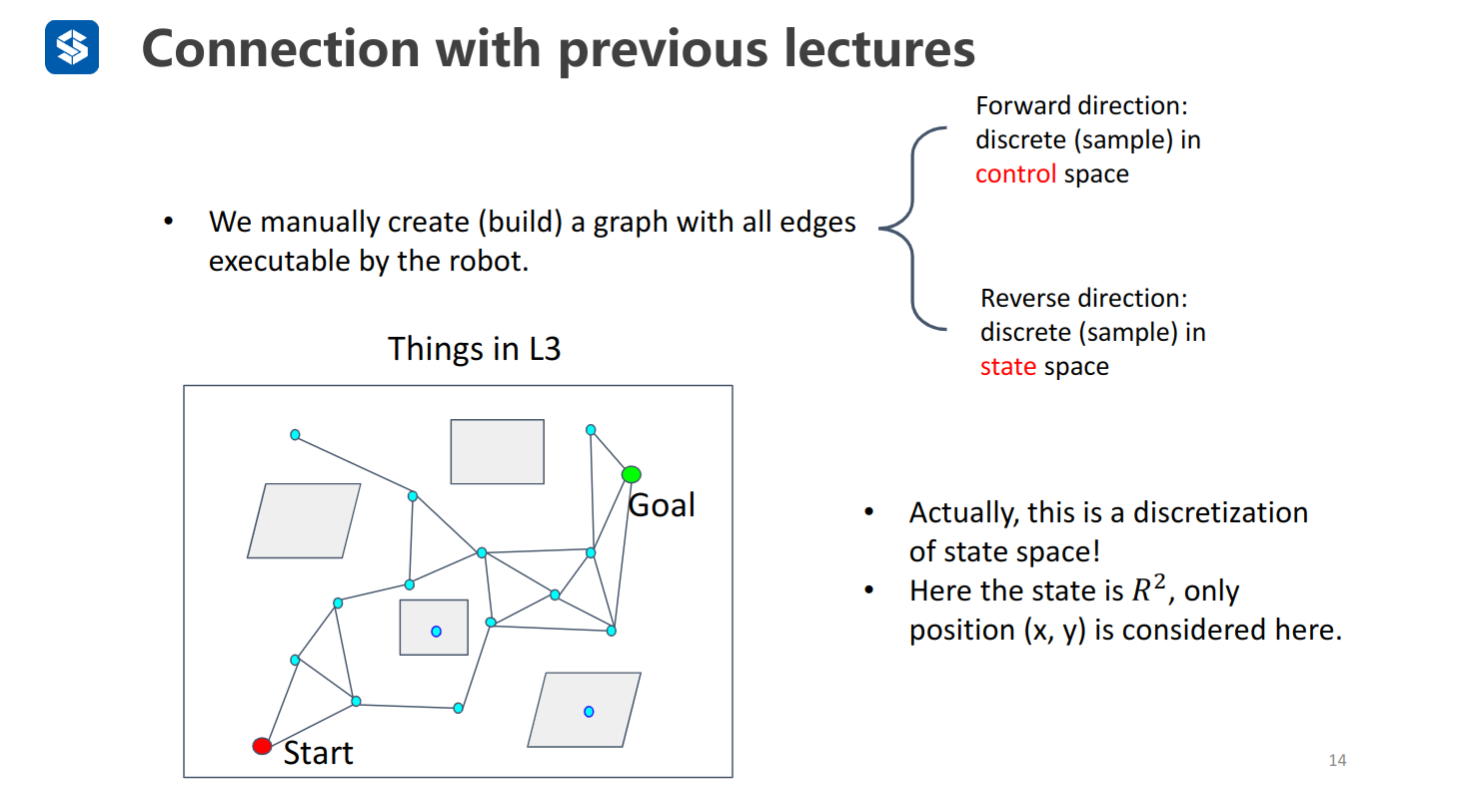
概率路图的散点可以看做离散了机器人的状态空间,再对点进行连接
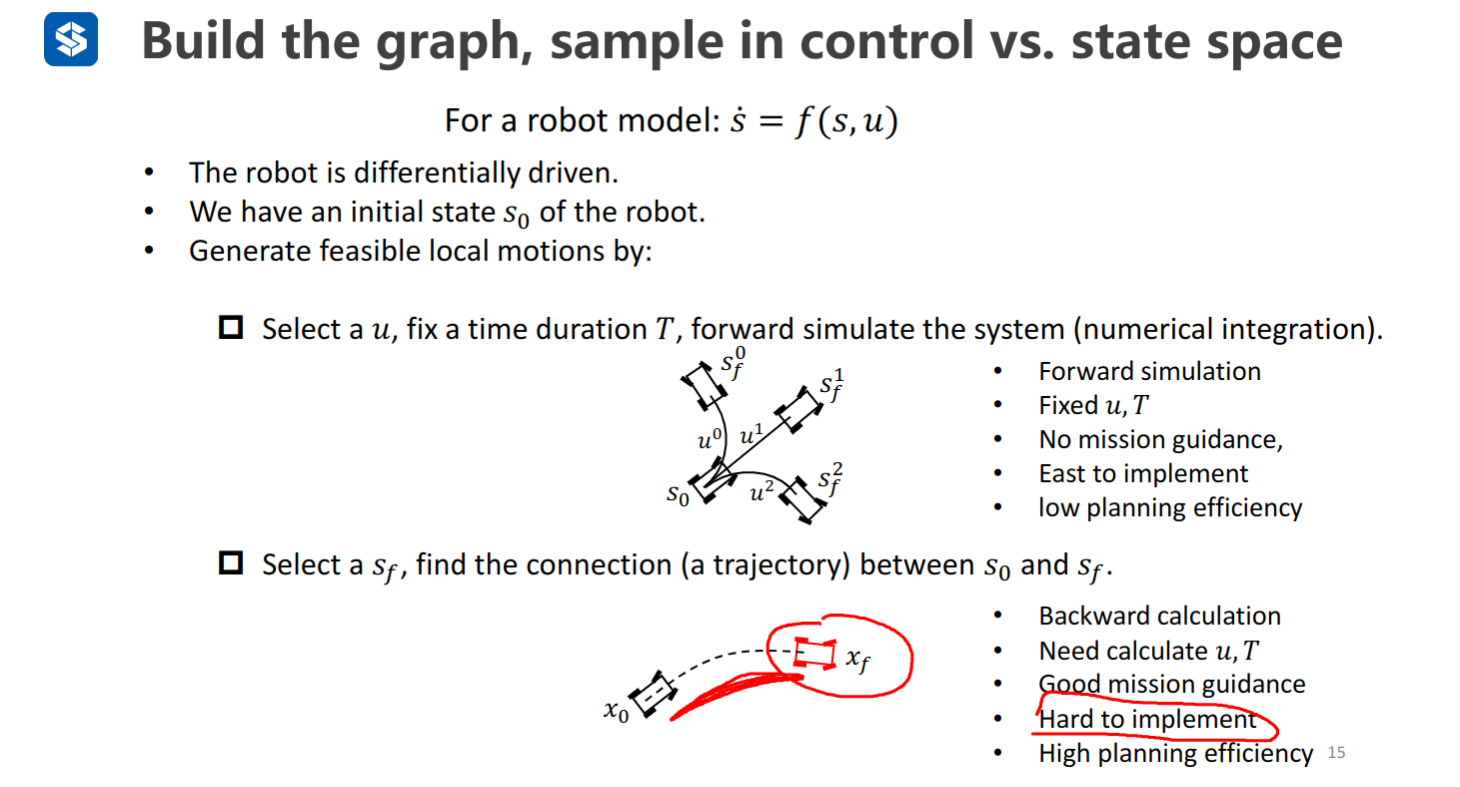
- 控制空间中采样:改变输入,固定一个时间
- 实现简单
- 规划低效,没有任务的导向性
- 状态空间中采样:改变输出,计算出时间和输入(求中间过程的 )
- 实现困难
- 任务导向性好
控制空间中采样
-
控制空间中采样示例
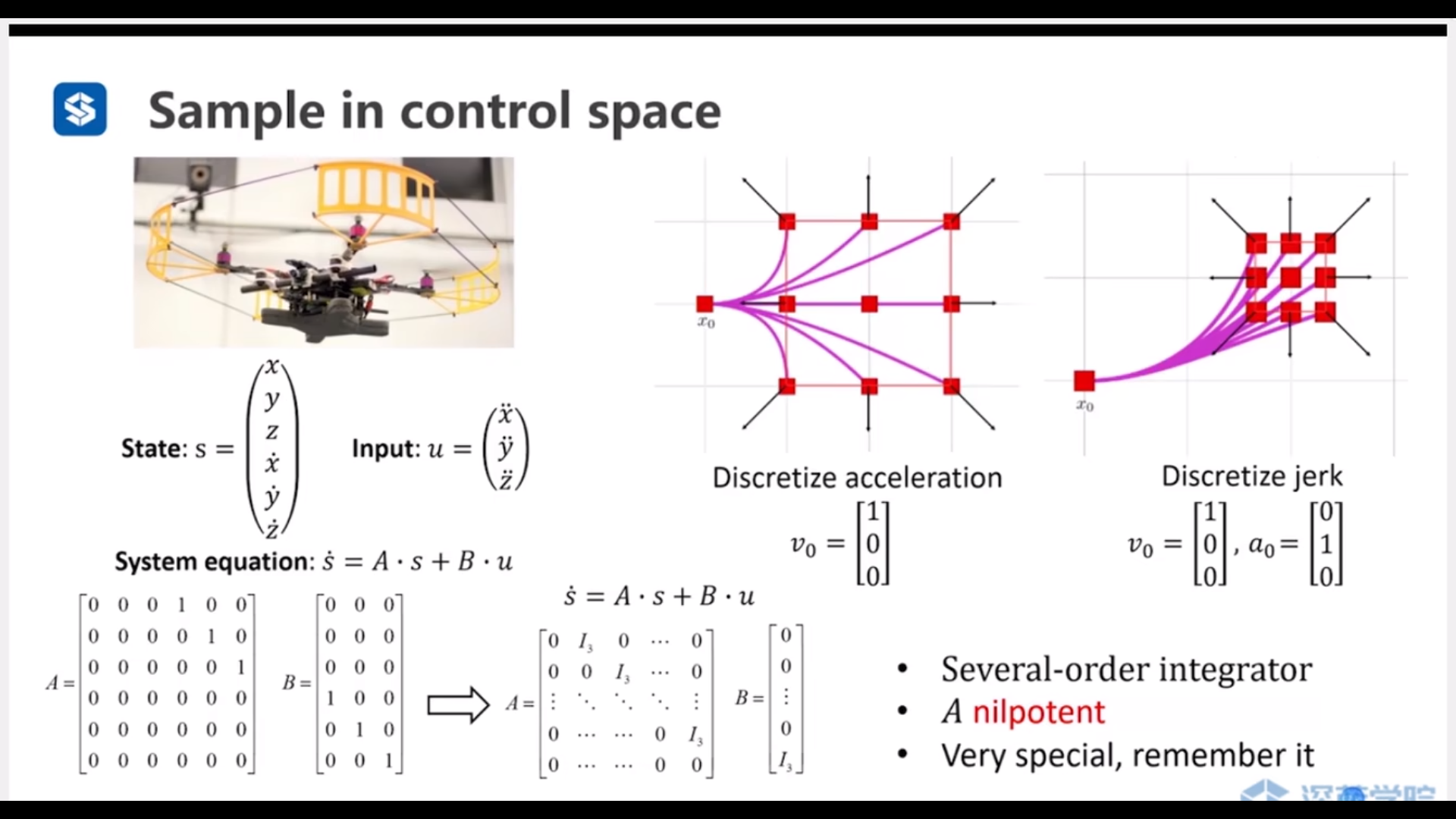
状态空间方程
是幂零矩阵(在线性代数中,对于阶方阵,存在正整数,使得,这样的方阵就叫做幂零矩阵。)
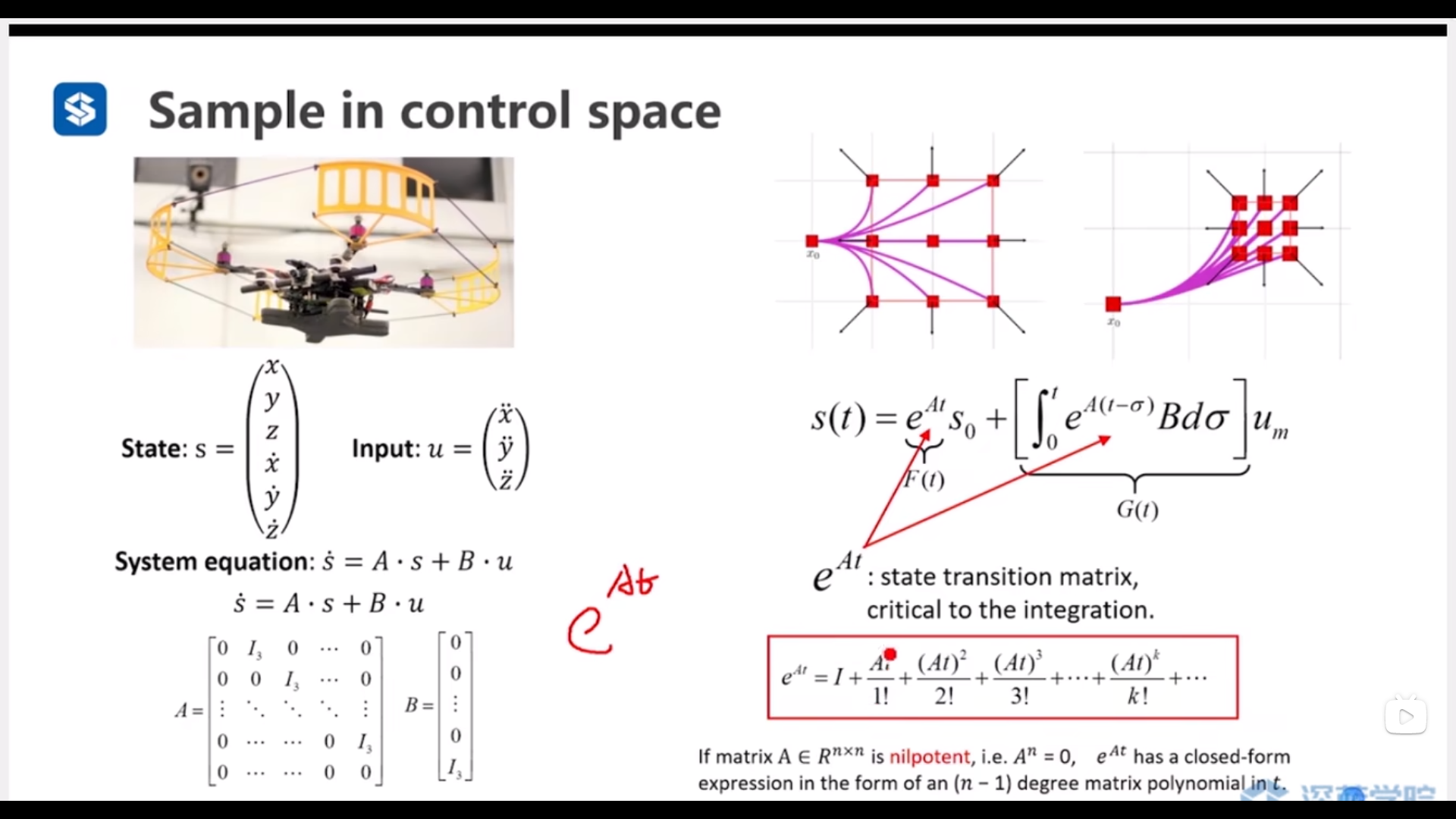
状态转移方程(得到中间状态)(为零输入相应,为零状态相应)
泰勒展开——利用幂零矩阵的性质

可以在搜索过程中建图——在拓展某个节点时才去创建邻居节点的状态,而不是说一开始直接建好整个栅格地图(节省时间和空间),有启发式函数
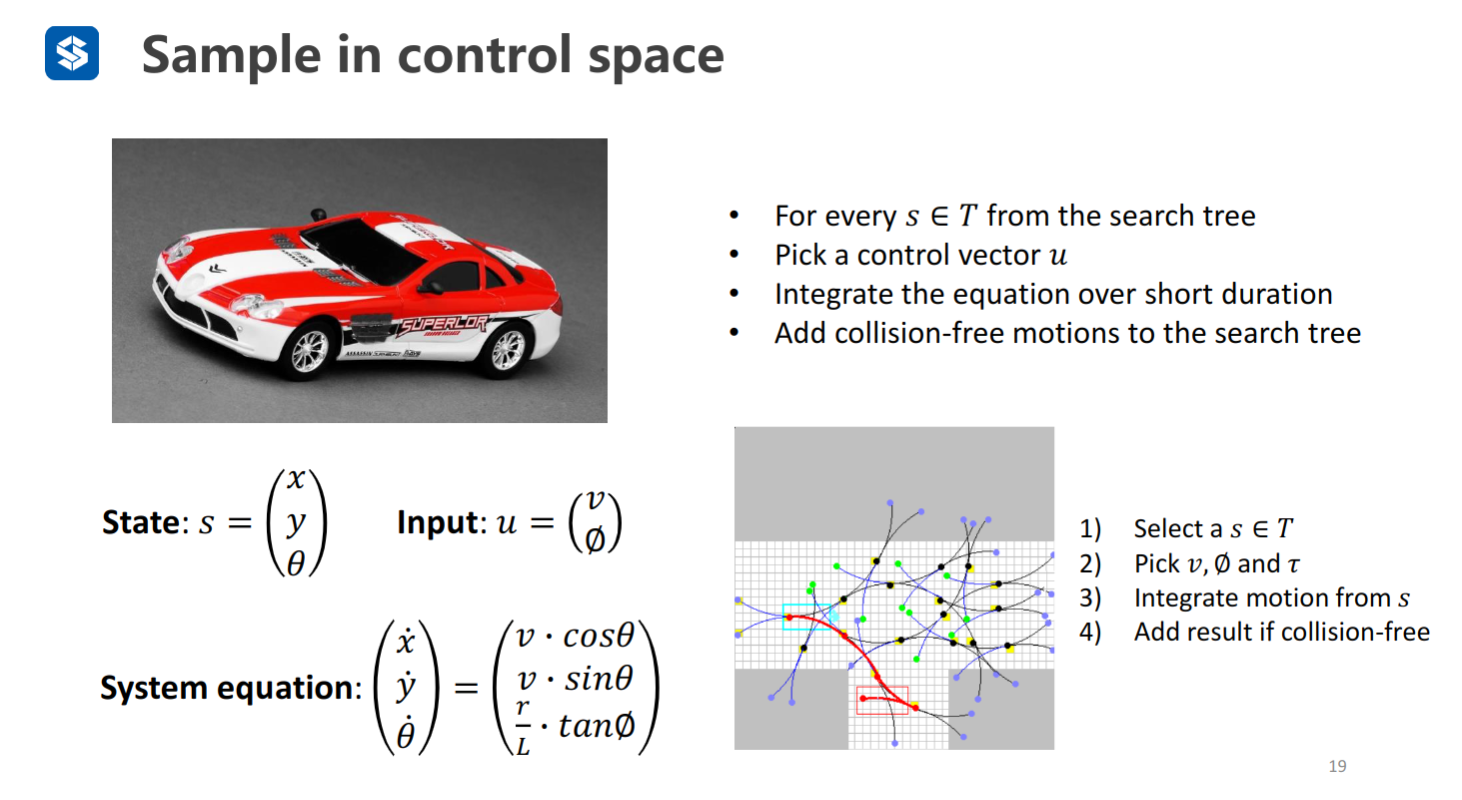
选择搜索树上的不同节点作为初始节点在状态空间中采样(不是一个规则的栅格图)
状态空间中采样
-
状态空间中采样示例
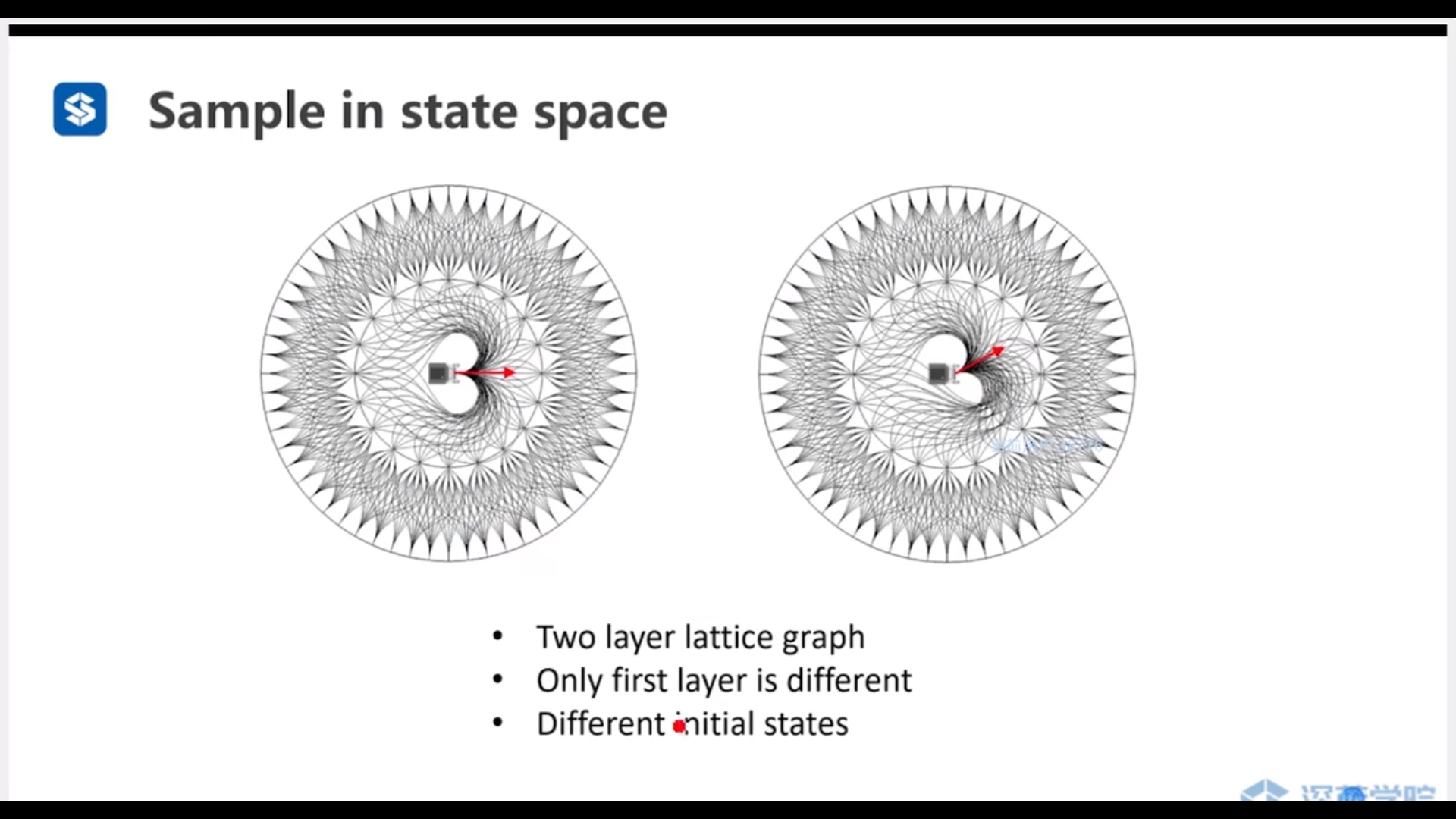
只有第一层是不同的(只有第一层涉及机器人的初状态,后面的层次都只涉及采样出来的状态点)
只需要实时生成局部的状态栅格图
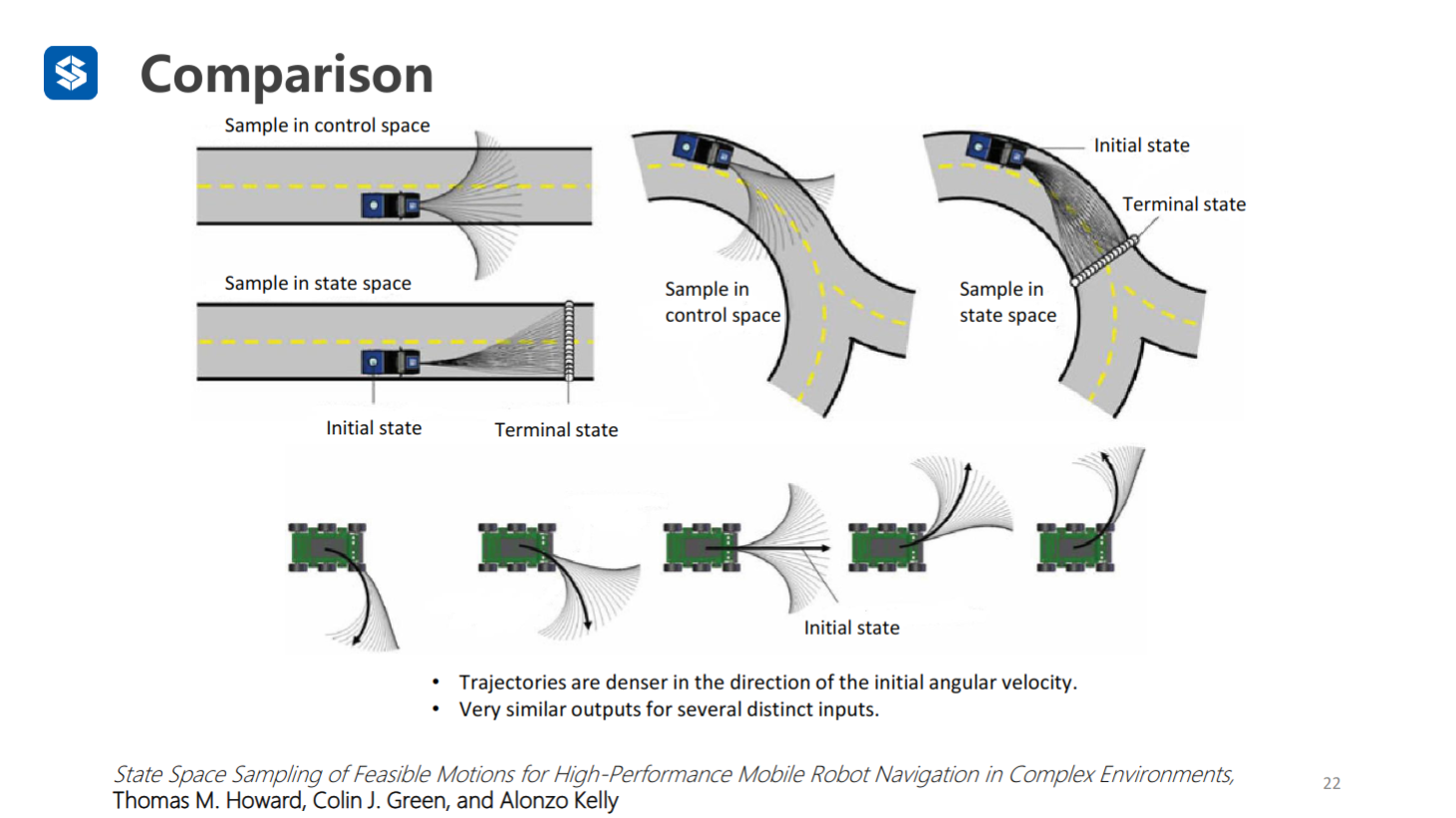
状态空间中采样往往是在一个固定的T和一系列固定的输入u下进行采样
控制空间中采样的问题:
- 没有目的性
- 轨迹在初始方向上更稠密
- 一些不同的输入产生的输出比较相似
两点边界最优控制问题(Boundary Value Problem——BVP)
-
示例
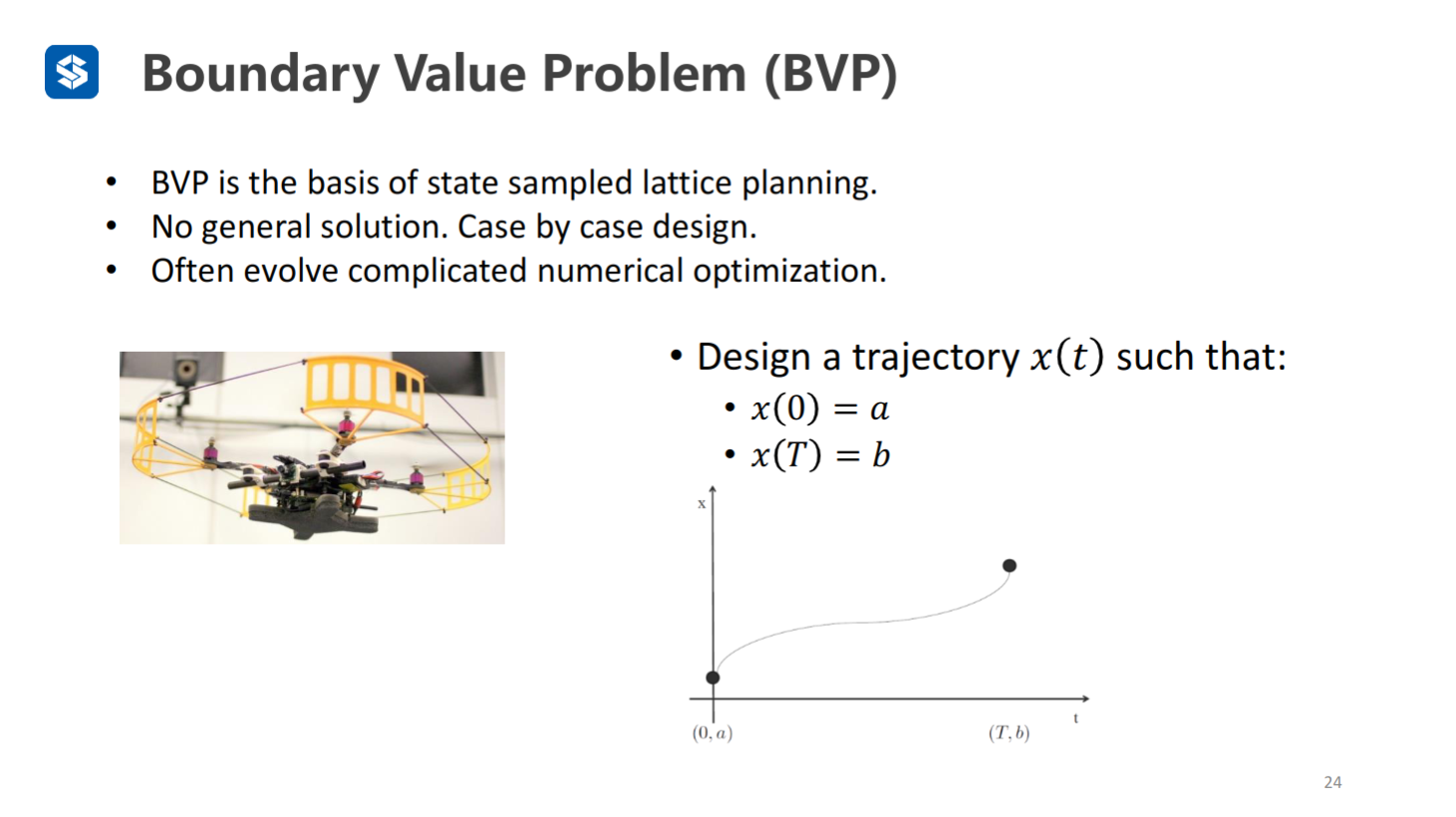

-
Modelling

目的:最小化jerk平方的积分
分成x,y,z三个维度,单独分析一个维度,简化问题
系统的输入为jerk,状态包含pos、velt、acc
-
minimum principle
庞特里亚金极小值原理
-
Solving
为谐态(谐态和System model是对应的,状态含多少个变量,谐态也应有相应的数量的变量)
汉密尔顿函数

最优控制问题的目标函数J——包含一个终末状态的惩罚项(例如停止时距离目标点的距离)和一个运行过程的代价项(例如运行过程能量损失)
是求偏导的意思(这里是指对s求偏导)
就是使后面这个式子达到最小值时的变量的取值

本例中为硬约束,故不用考虑终末状态的惩罚项,也没有极小值原理的边界条件
当取得最优状态时,均为最优,故要求使最小的输入变量时,可以直接忽略掉本式子中、项的作用
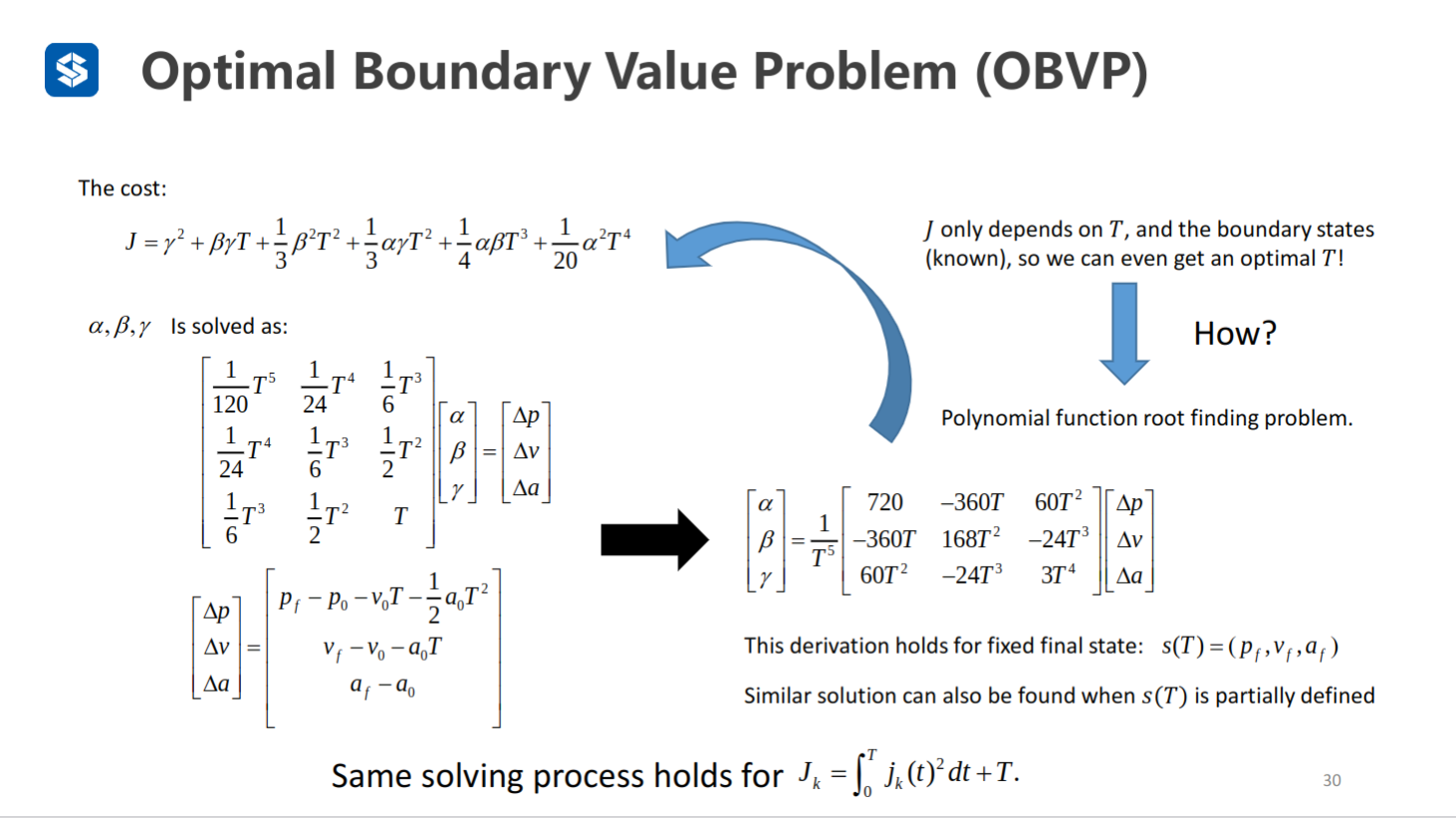
最后用末尾时刻的边界条件来确定
是与时间T有关的值,且确定后,目标函数也可以确定(变成和时间有关的函数),可以对这个式子求导,得到最优时间(多项式求根的问题)


局部路径规划,可以使用轨迹库
对不同轨迹打分,看看选择那个轨迹

可以设计一个不考虑障碍物的启发式函数或者一个不考虑动力学的启发式函数 对于避障来说,在上图中不考虑动力学的启发式函数的效果比不考虑障碍物的启发式函数的效果好
在工程中,可以选择两个共同作用,或取两个中的最大值作为启发式函数
混合A算法(Hybrid A)
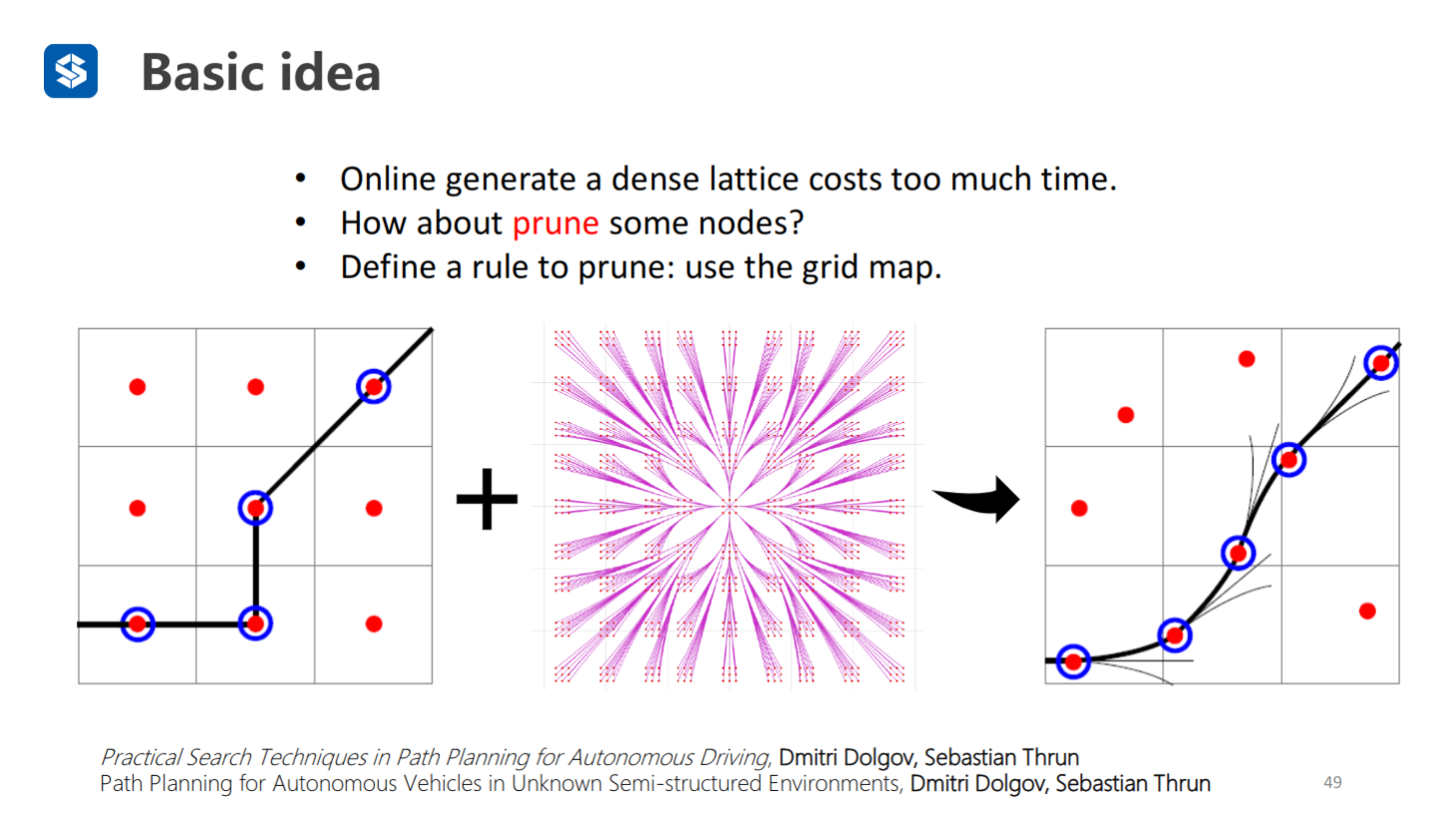
实时生成一个稠密的栅格地图时间开销较大
可以利用栅格地图剪枝(每个栅格只保留一个节点)
判断同一个栅格中新出现的状态能否替代原来的状态的依据:新的节点能否减小整个路径上的代价函数(广义的代价——最优控制)

寻找邻居节点的方法:前向积分节点中的状态(离散控制空间),寻找可以演化出来的邻居节点
记录节点m的状态、更新节点m的状态(混合A和A主要的不同之处)
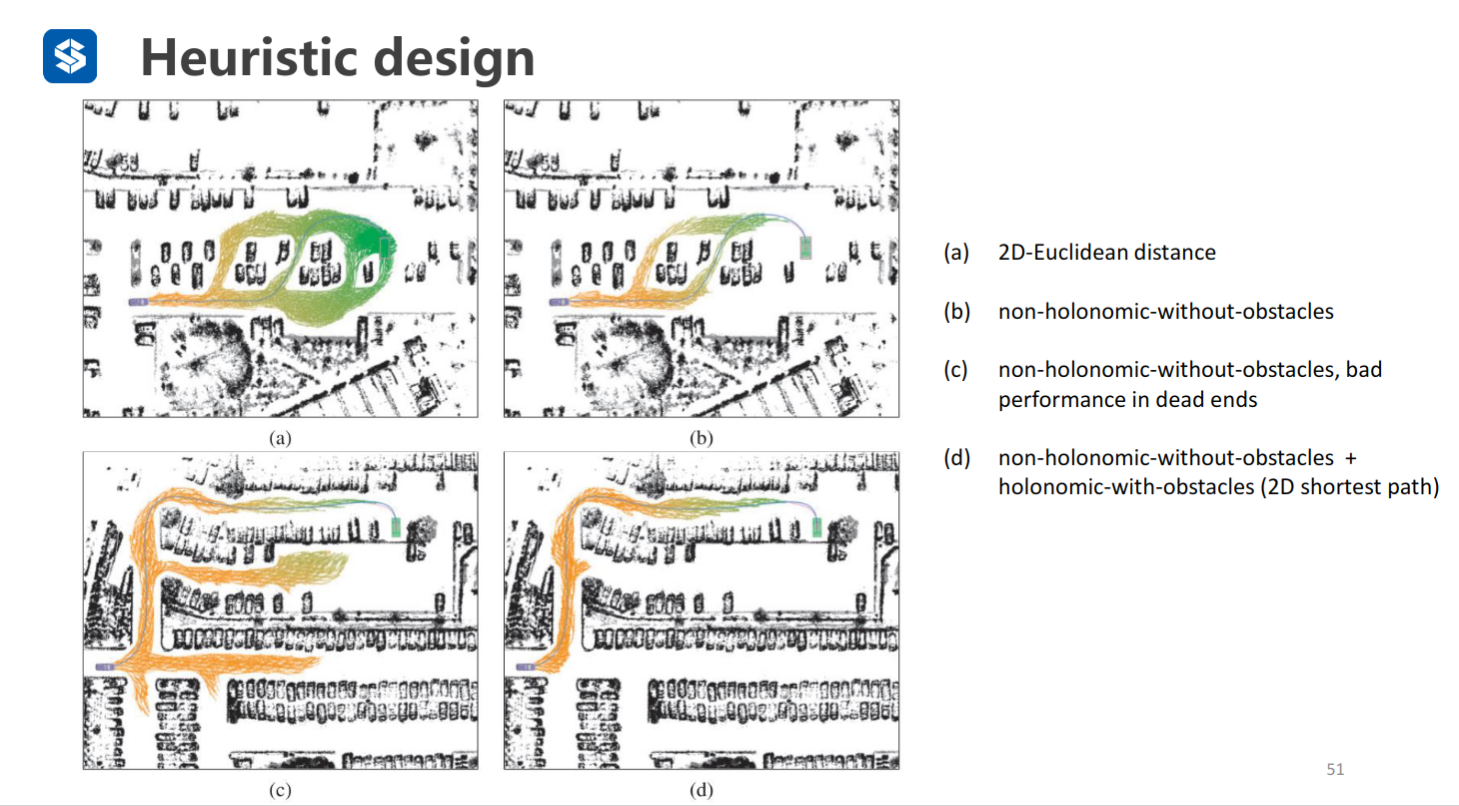
考虑动力学但不考虑障碍物的启发式函数+考虑动力学但不考虑障碍物的启发式函数
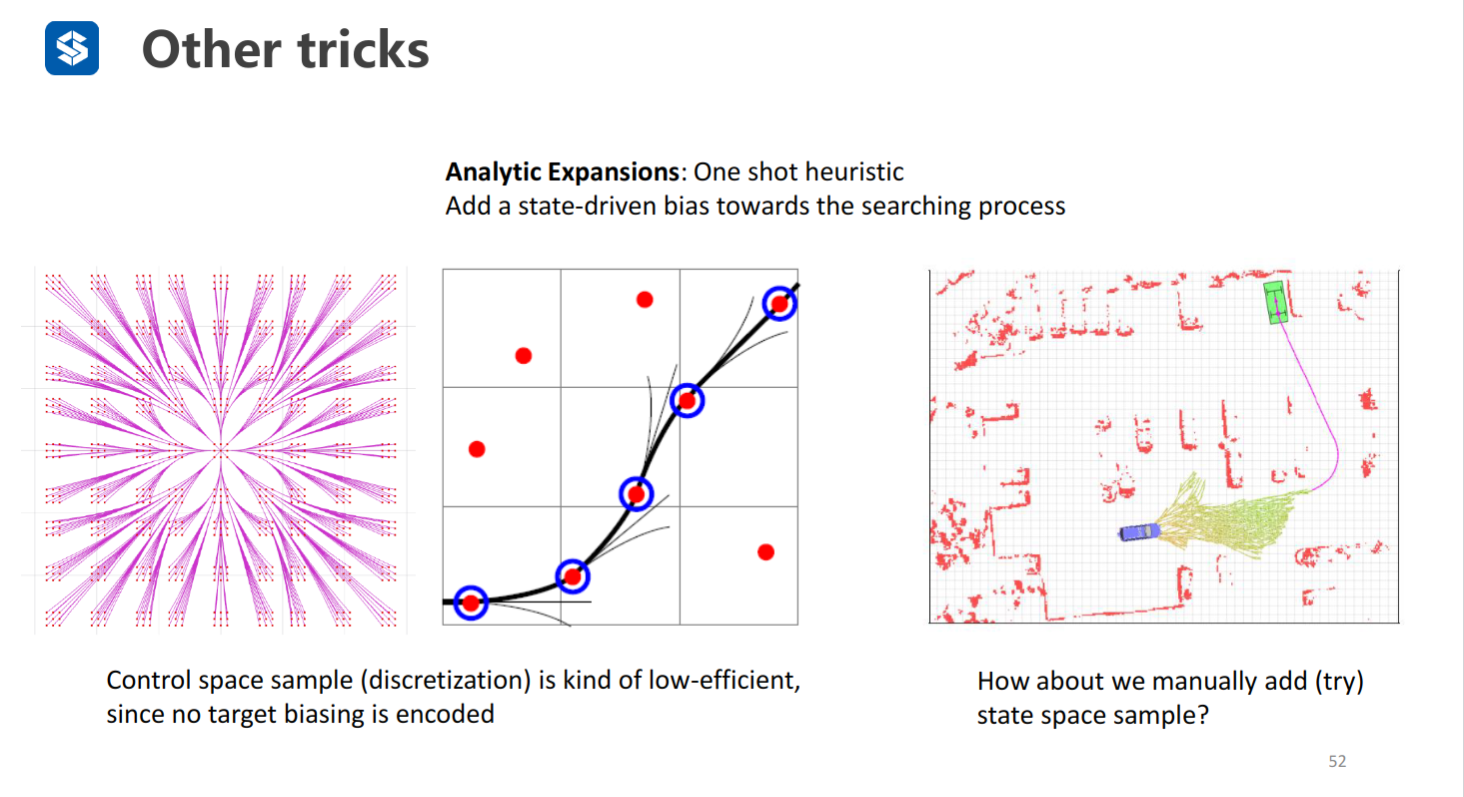
在生成路径的过程中,在某些节点尝试能否直接用OBVP找到一条到终点的路径(无障碍物),如果找到了,就能直接结束路径搜素(一种比较合理的方法——在一开始时,尝试的次数可以较少,随着接近终点时,增大尝试次数)
动力学约束RRT*(Kinodynamic RRT*)
-
How to Sample
在整个状态空间进行采样,采样后直接得到,而不需要像RRT*从采样点向最近点移动一段距离
-
How to define Near
用最优控制的方法将邻近节点和采样的节点连接(可以使用OBVP中的方法(庞特里亚金极小值原理)进行最优控制),也可以采用如下的方法

R是权重(决定时间项()和能量项()的权重)

利用李雅普诺夫方程求得最优控制的输入

得到零输入响应

求得最优控制的代价函数,并对求导得到最优的时间
-
How to ChooseParent

RRT是按距离选出邻域,而KRRT是按代价选择出邻域(正向可达集、反向可达集)
并且可以用kd-tree的形式存储,方便查询


]是一个以x为中心的椭圆,因此前向可达集是对所有可能时间的高维椭圆的并集

为了简化问题,可以通过高维椭圆得到外接边界框,进而计算出每个维度上的最大和最小值
-
How to Rewire

Rewire关心从x_rand节点可以到哪些节点(前向可达集);ChooseParent关心哪些节点可以到达x_rand(后向可达集)
