基于图搜索的路径规划
图搜索基础:

机器人的配置、机器人的自由度、机器人的配置空间

把工作空间中的障碍物转化为配置空间中的障碍物——障碍物膨胀(在运动规划之前进行)
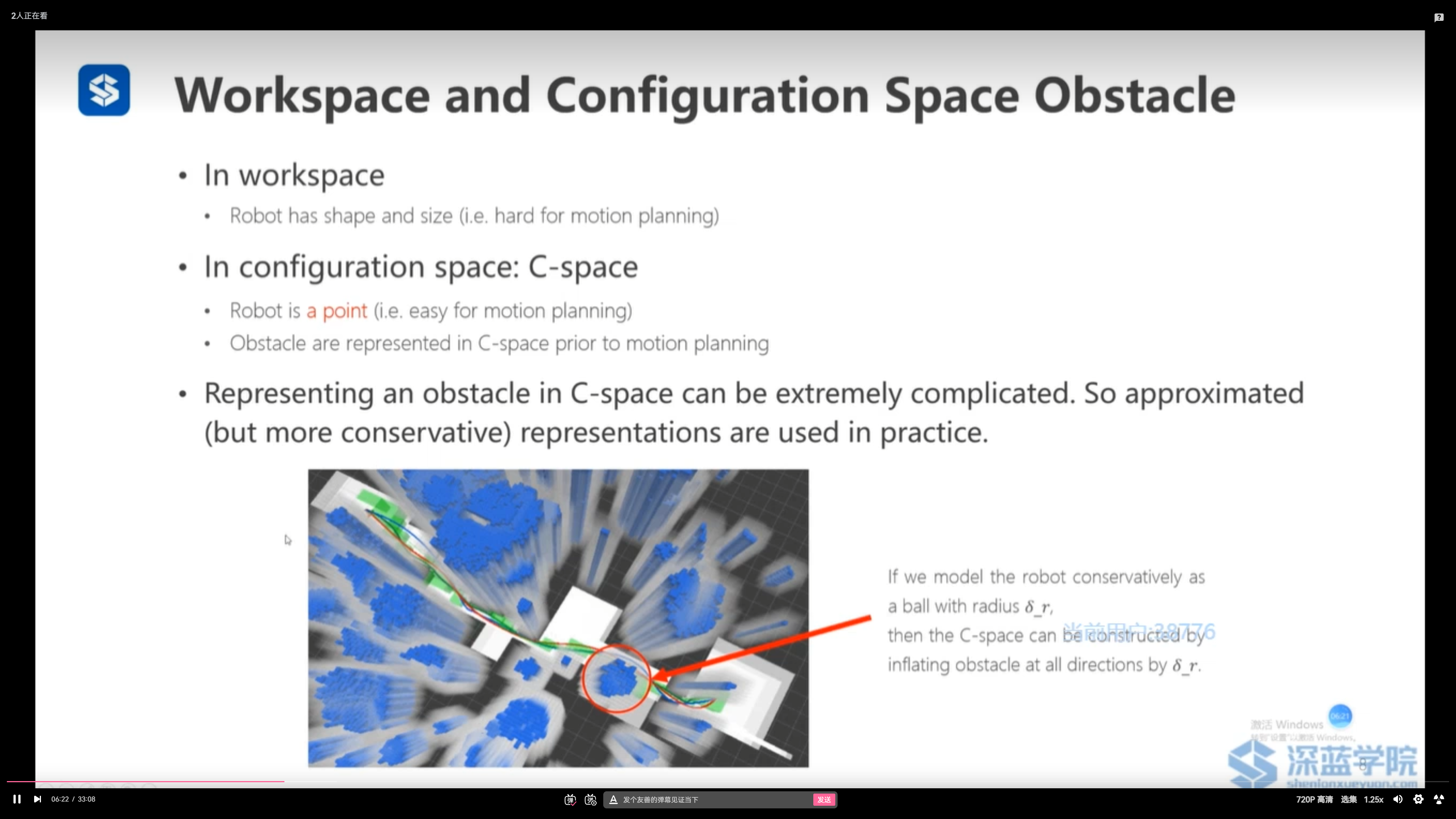
路径规划是在机器人的配置空间下进行的——机器人可以看做一个质点

对于任何一个搜索算法:构造搜索图
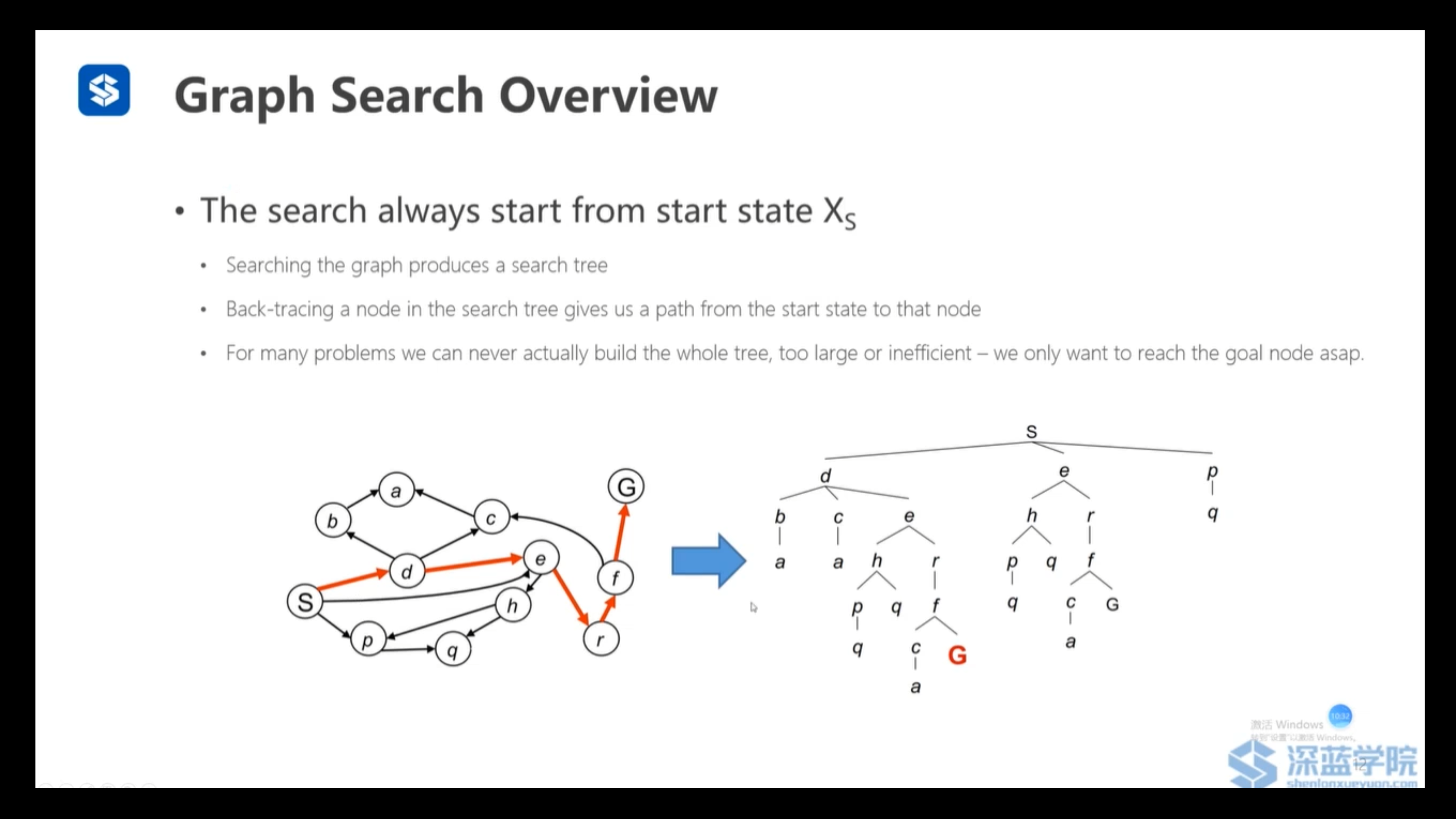
搜索图提供了搜索树,回溯节点得到路径
图搜索算法总体框架:

- 维护一个存储所有要访问的节点的容器
- 这个容器用起始节点初始化
- 循环
- 根据某些指标访问容器中的一个节点(Visit and Remove)
- 扩展节点:包含该节点的所有邻居
- 把邻居节点塞回容器
- 结束循环

访问过的节点不能再访问
BFS和DFS算法:
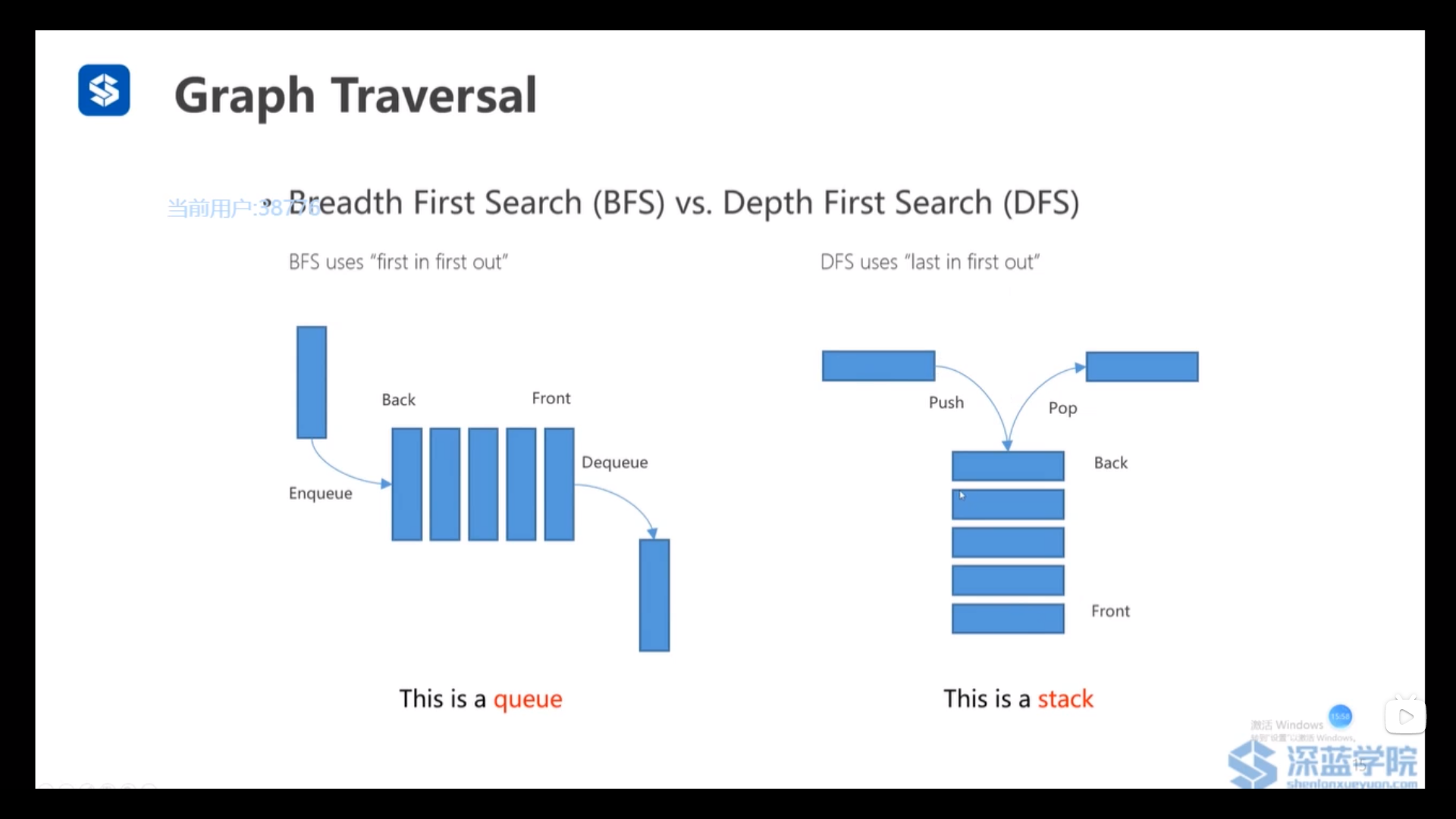
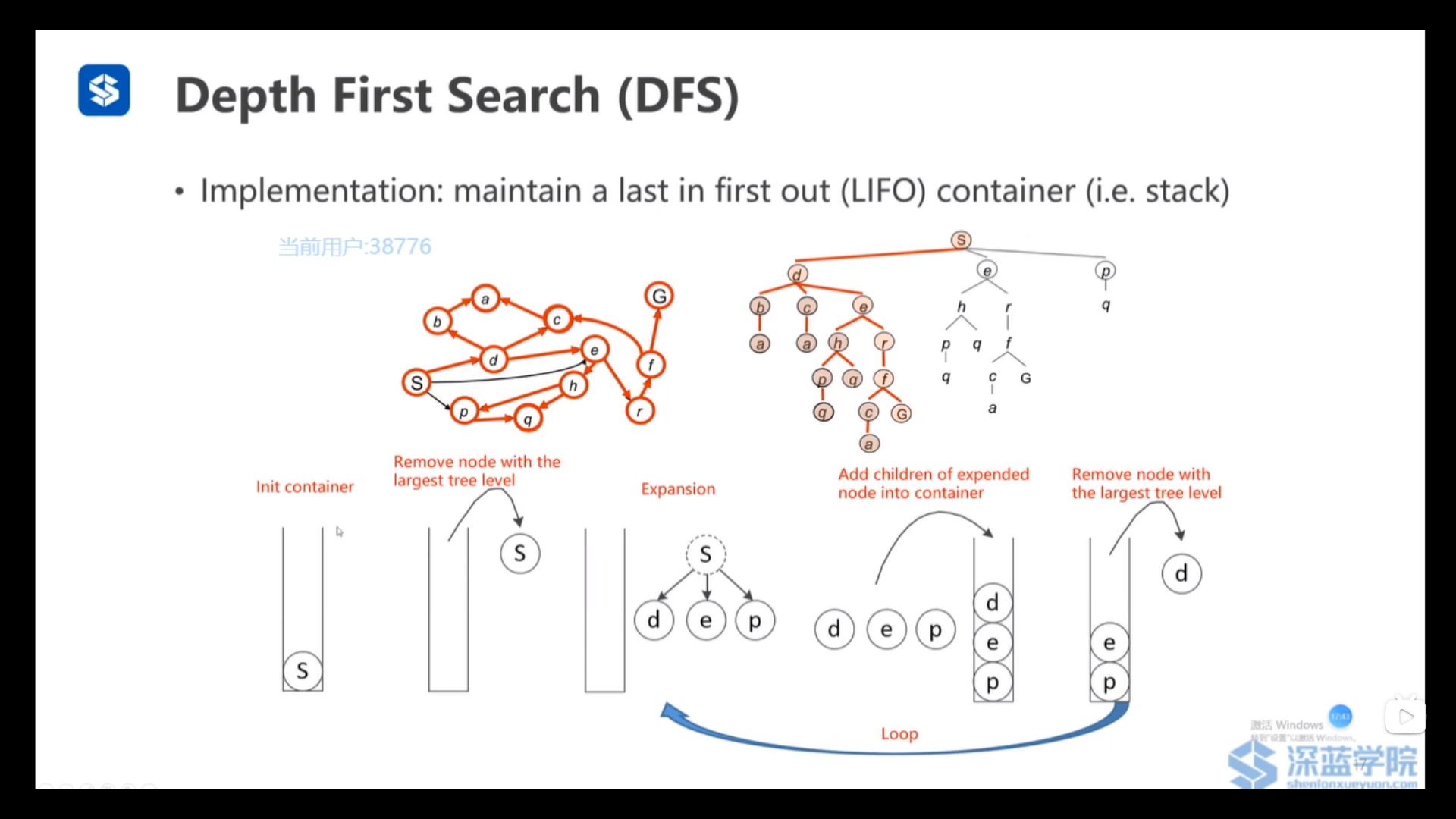
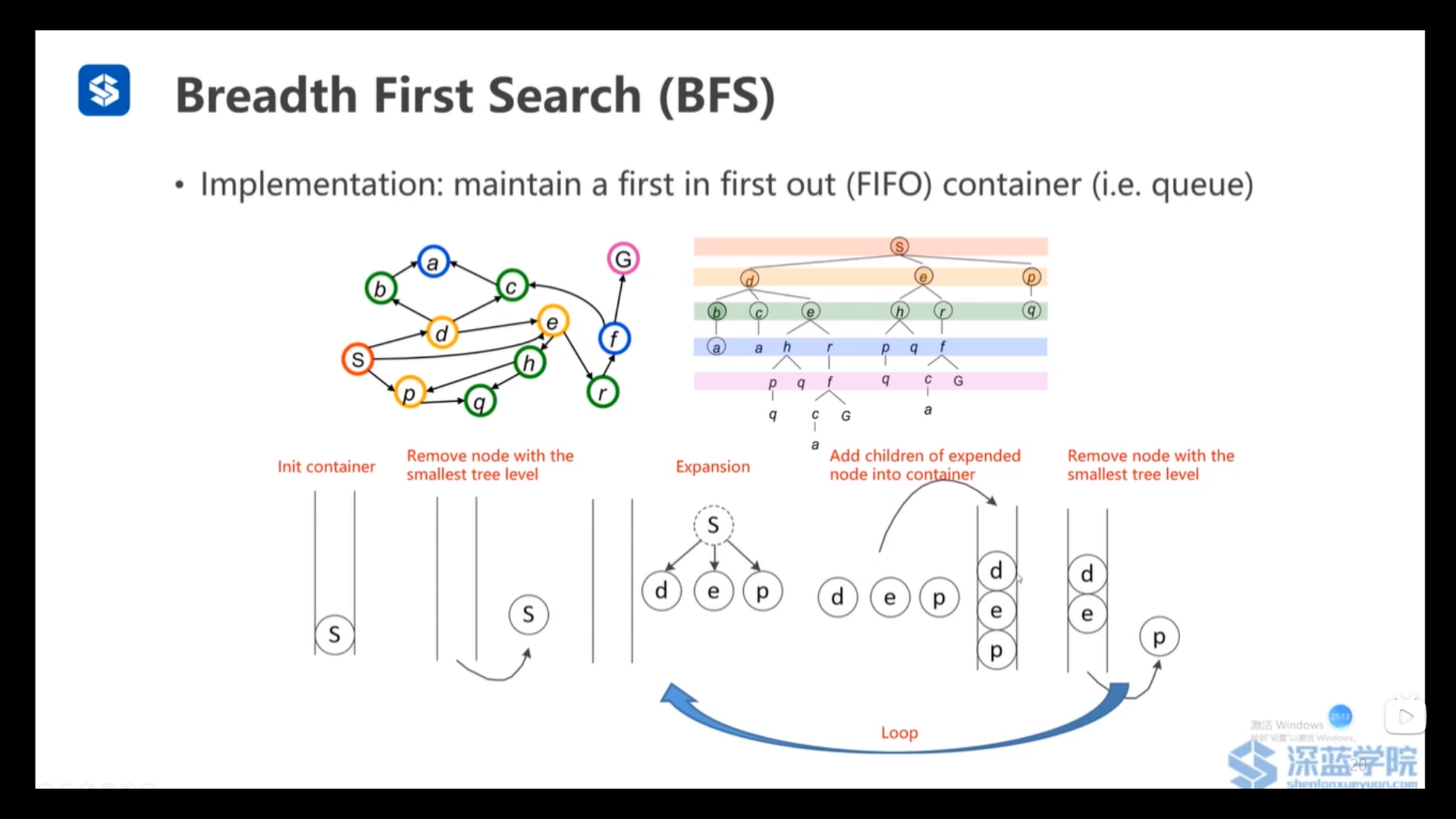
深度优先搜素(DFS):维护的是一个栈(后进先出)——每次访问容器中深度最深的节点
广度优先搜素(BFS):维护的是一个队列(先进先出)——每次访问容器中深度最浅的节点

分析上图,可知:图搜索的基础应该是BFS——可以得到最短路径
Greedy Best First Search:
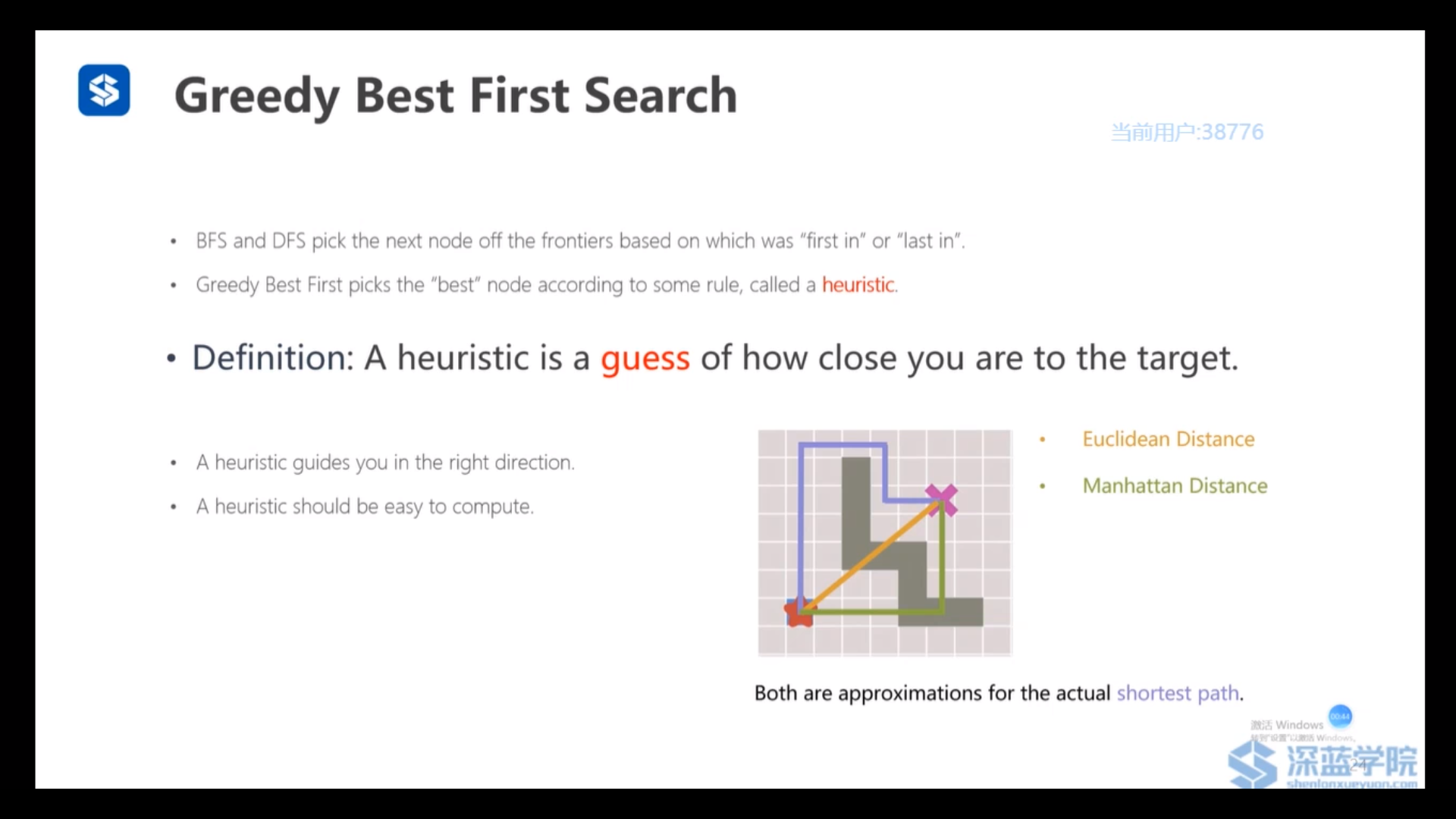
贪心算法有很强的目的性,得到的是局部最优解,不一定是全局最优解。

Dijkstra和Astar算法:
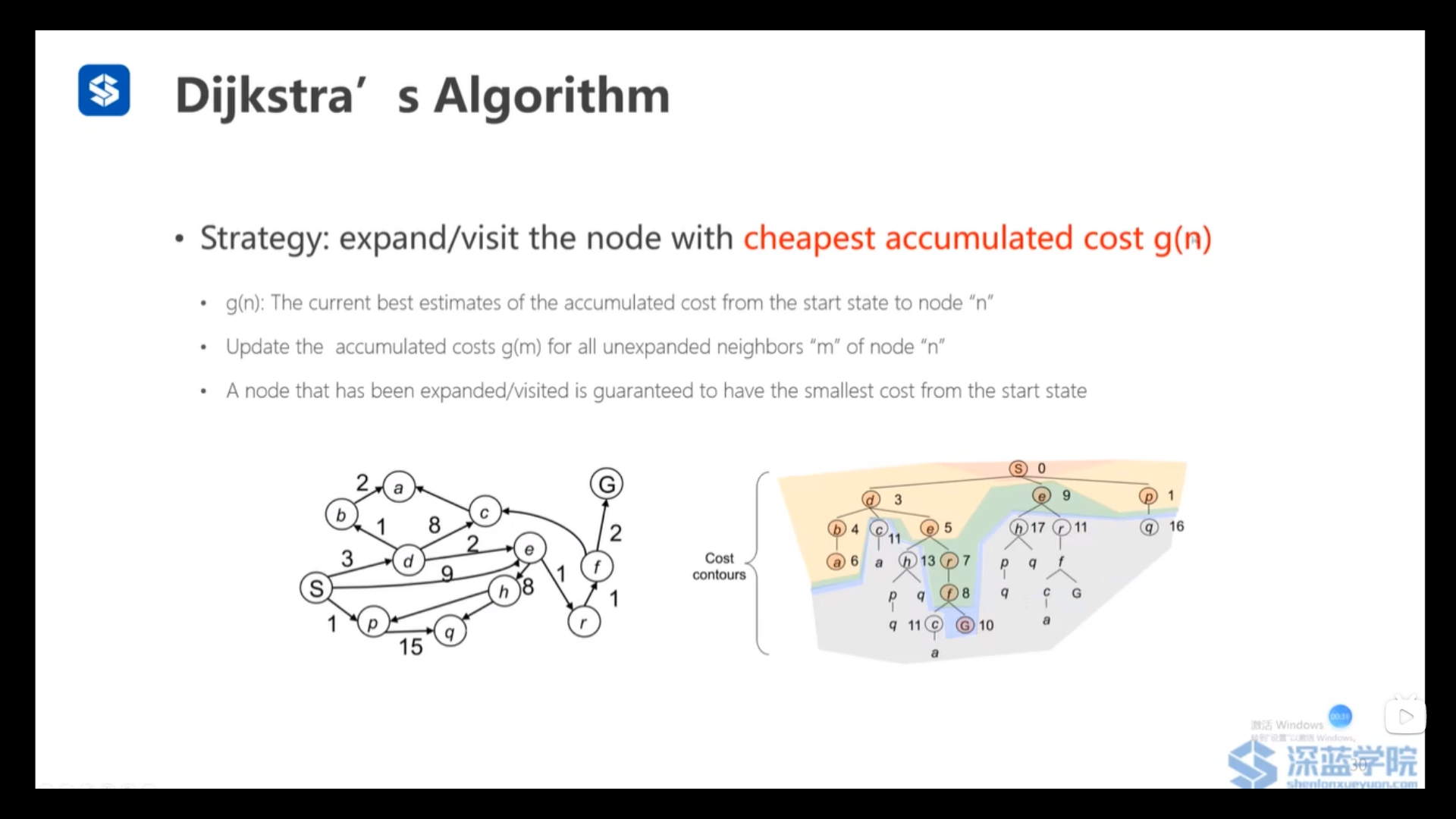
Dijikstra算法是根据代价g(n)来弹出节点,g(n)为从起点出发到当前节点的代价和
同时尝试能否通过节点n来更新n的邻居m的代价g(m)

维护一个优先级队列的容器
如果g(m)为inf,说明m为被放到容器中;如果g(m)为有限值,说明m已经被添加到容器中

Dijkstra在代价均为1的情况下,和BFS是等价的,是均匀扩散的
Search Heuristics
- 添加了对到目标节点代价推测的启发式函数(goal cost)
- 例如:
- 曼哈顿距离
- 欧式距离

g(n)和Dijkstra中的一样
h(n)——估计的到目标节点的代价(goal cost)


A*算法如果要保证最优性,必须要求所有节点的估计到终点的最小代价小于等于实际到终点的最小代价
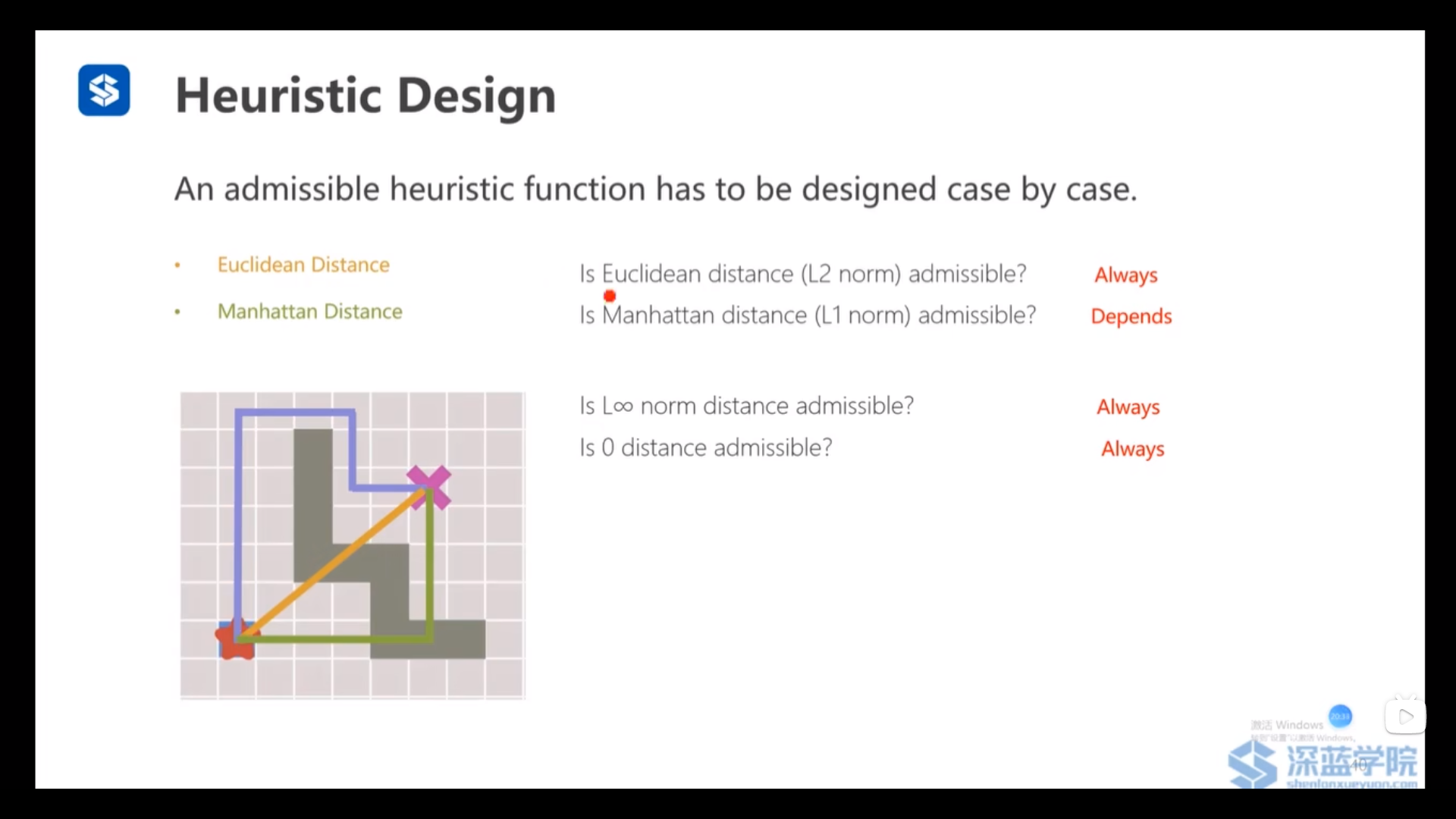
可用的启发式函数(L1 norm 曼哈顿距离、L2 norm 欧式距离、L-inf 给出向量中最大的值)
曼哈顿距离:
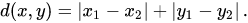
欧式距离:
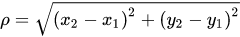

Weighted A*:在启发式函数上加权,以次优性换取快速性
解的代价≤系数*最优的代价(论文中有证明)
测试动画:
http://qiao.github.io/PathFinding.js/visual/
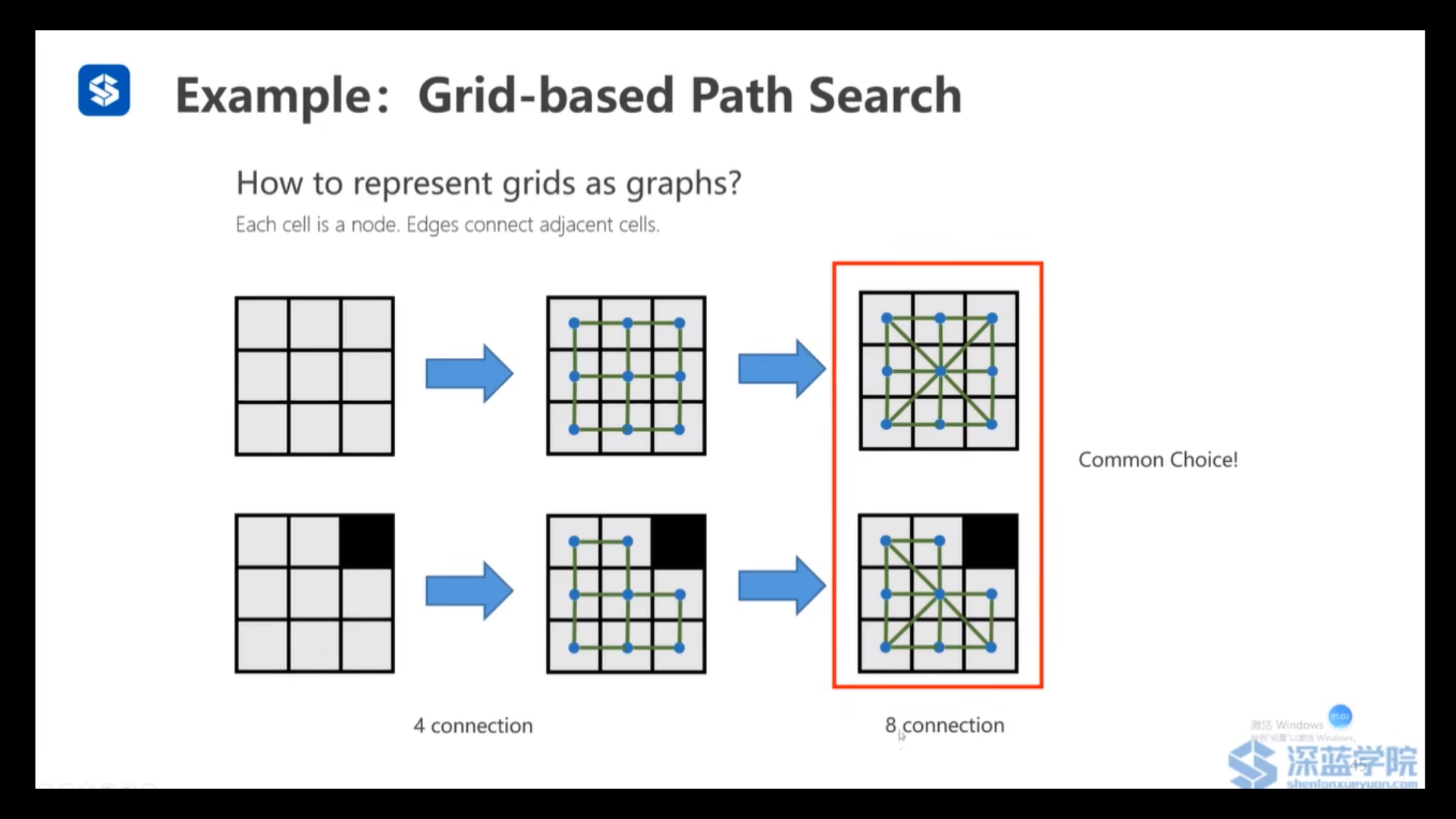
栅格地图转化为图结构(四连接、八连接)

在C++中表示优先级队列——std::priority_queue、std::make_heap、std::multimap
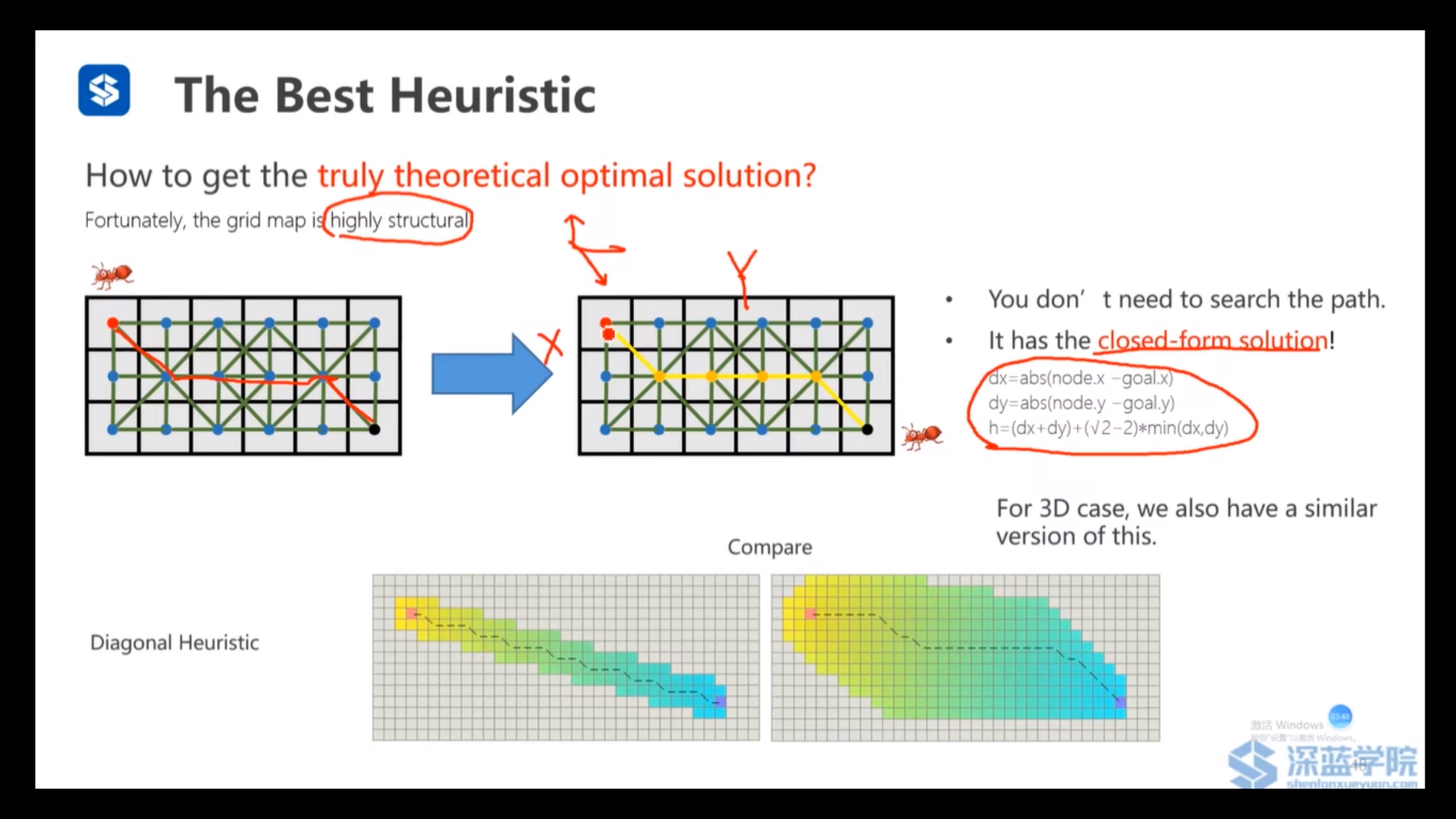
八分叉的栅格地图最优的启发式函数(对角线启发式函数),对于3D的情况,同样可以设计一个对角线启发式函数。
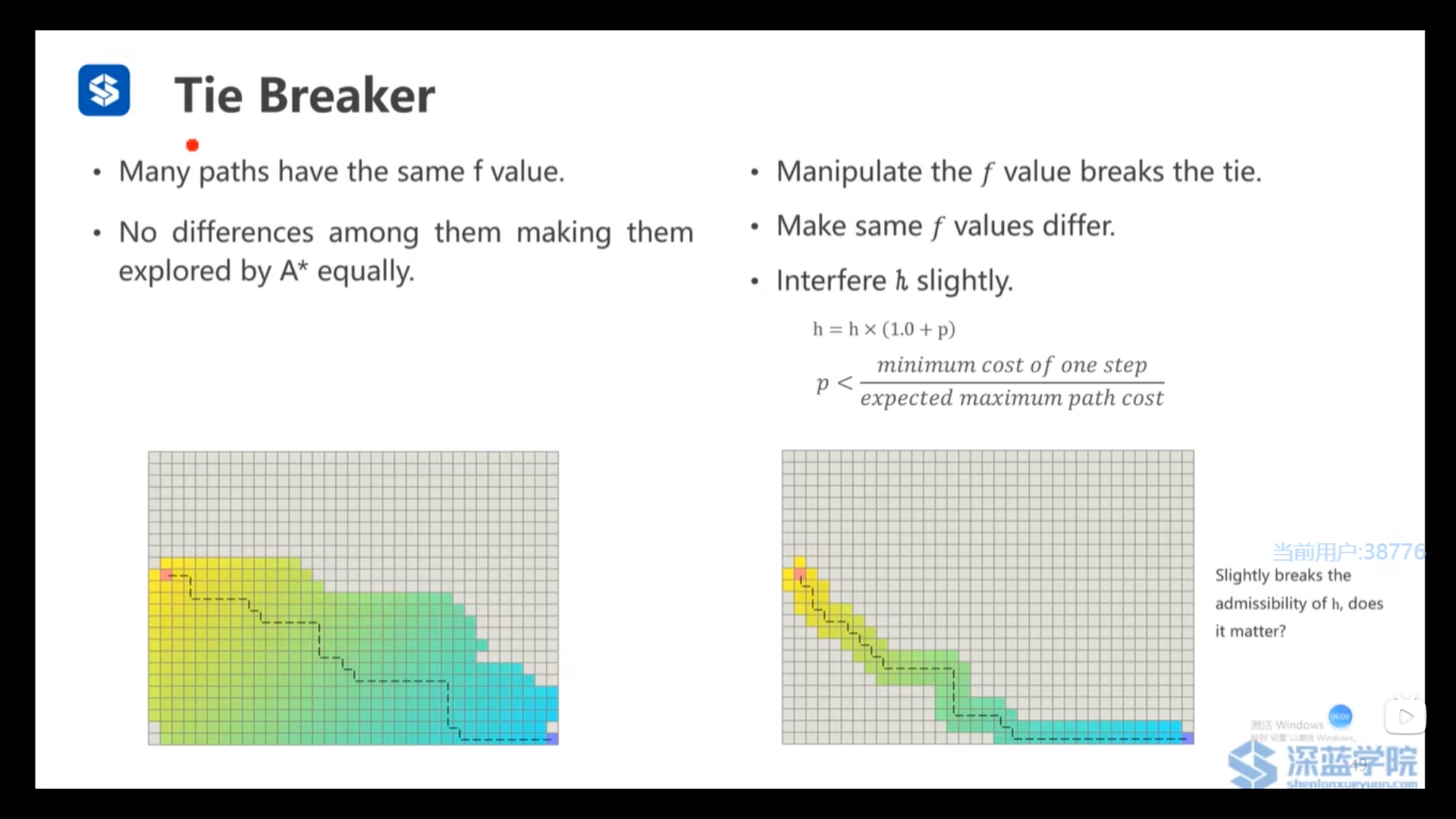
Tie Breaker(平衡性打破)——用来打破均匀扩展的问题
- h=h*(1.0+p)
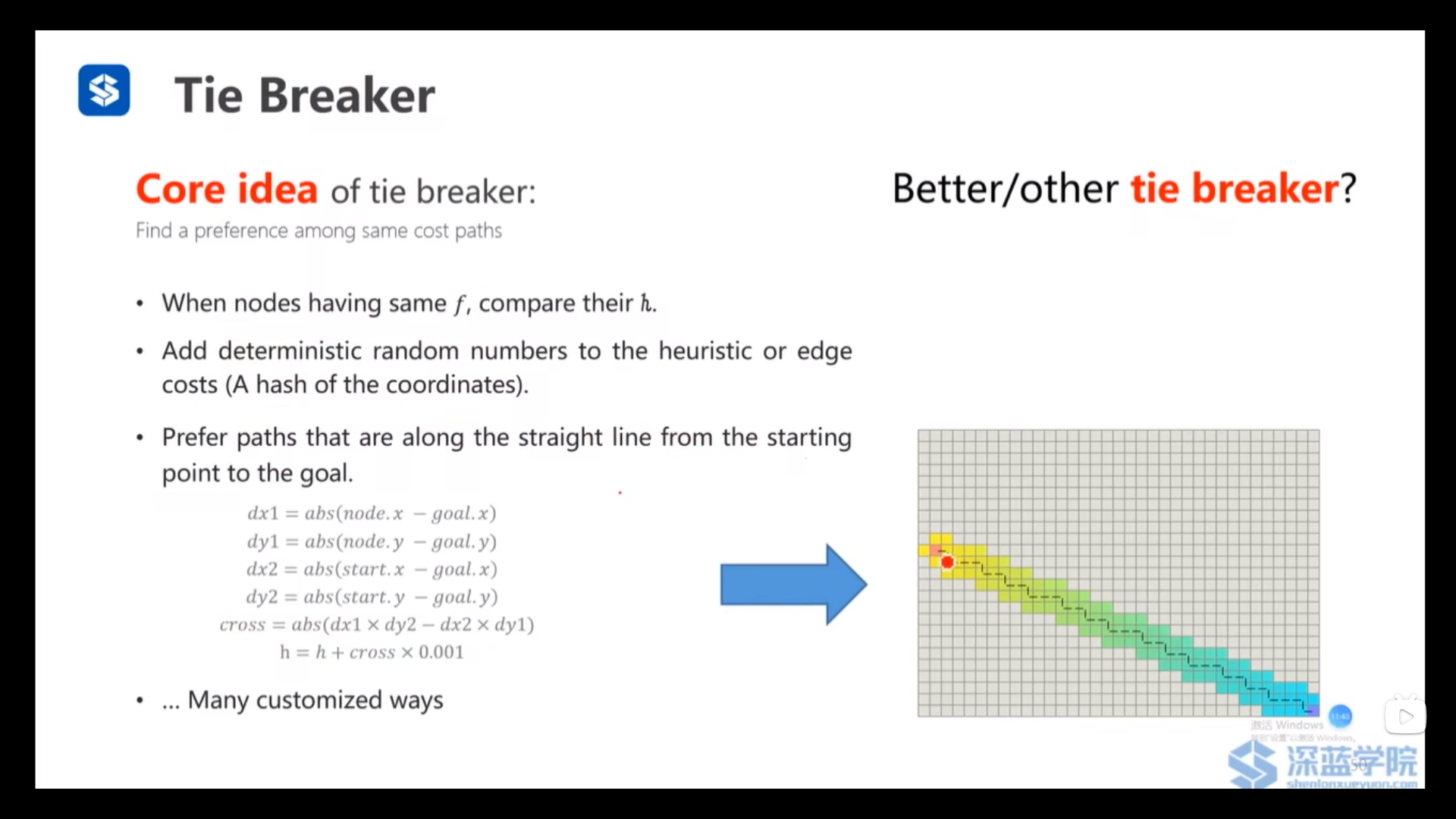
- 添加一个随机哈希值给启发式代价或者边的代价
- 添加一个离直线距离(从起点到终点)远近的代价
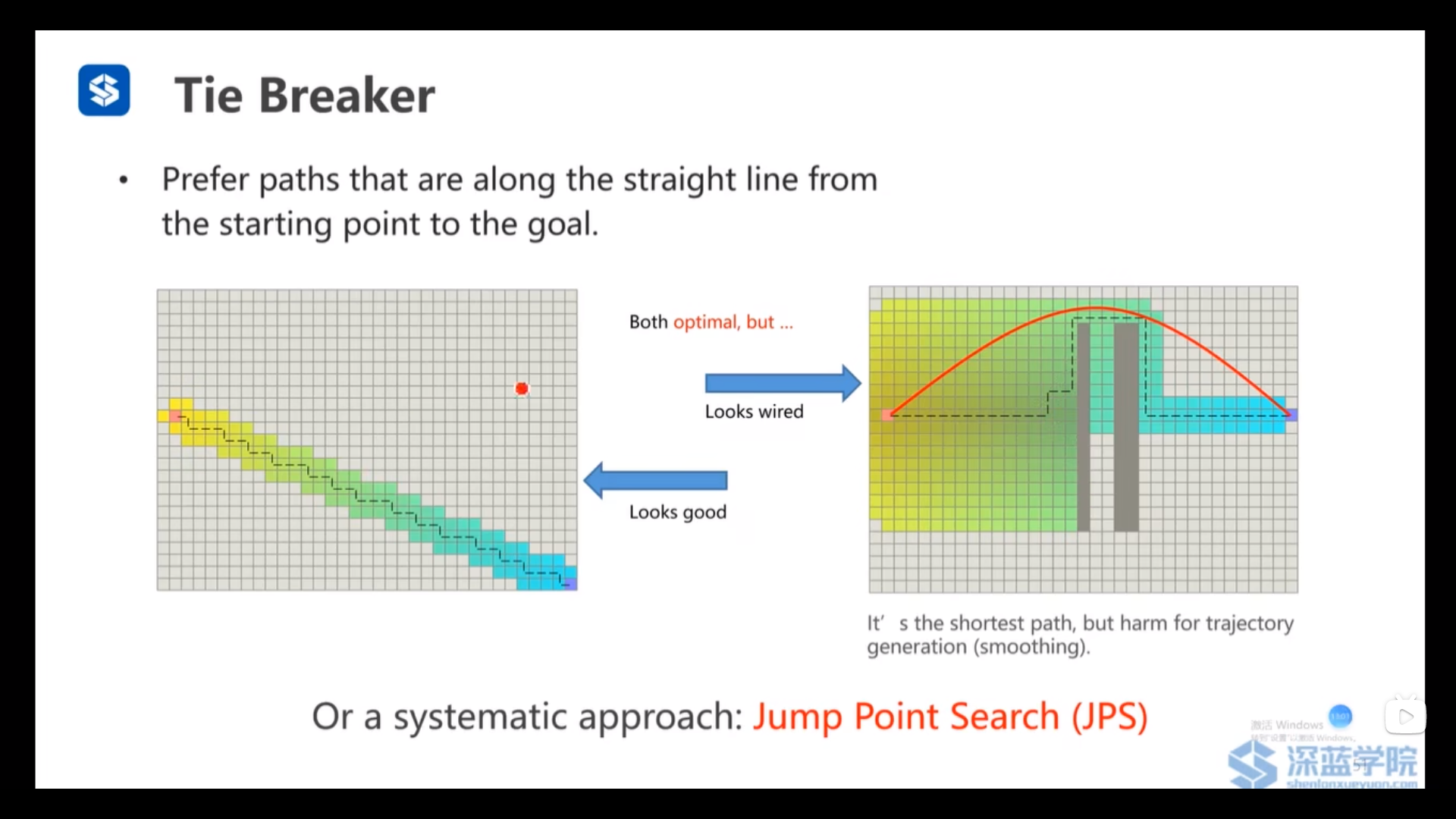
但Tie Breaker可能会导致生成的Path不适合轨迹生成(平滑性不好),具体使用怎样的Tie Breaker需要在工程中测试
JPS算法:
JPS算法的核心:找到并打破对称性
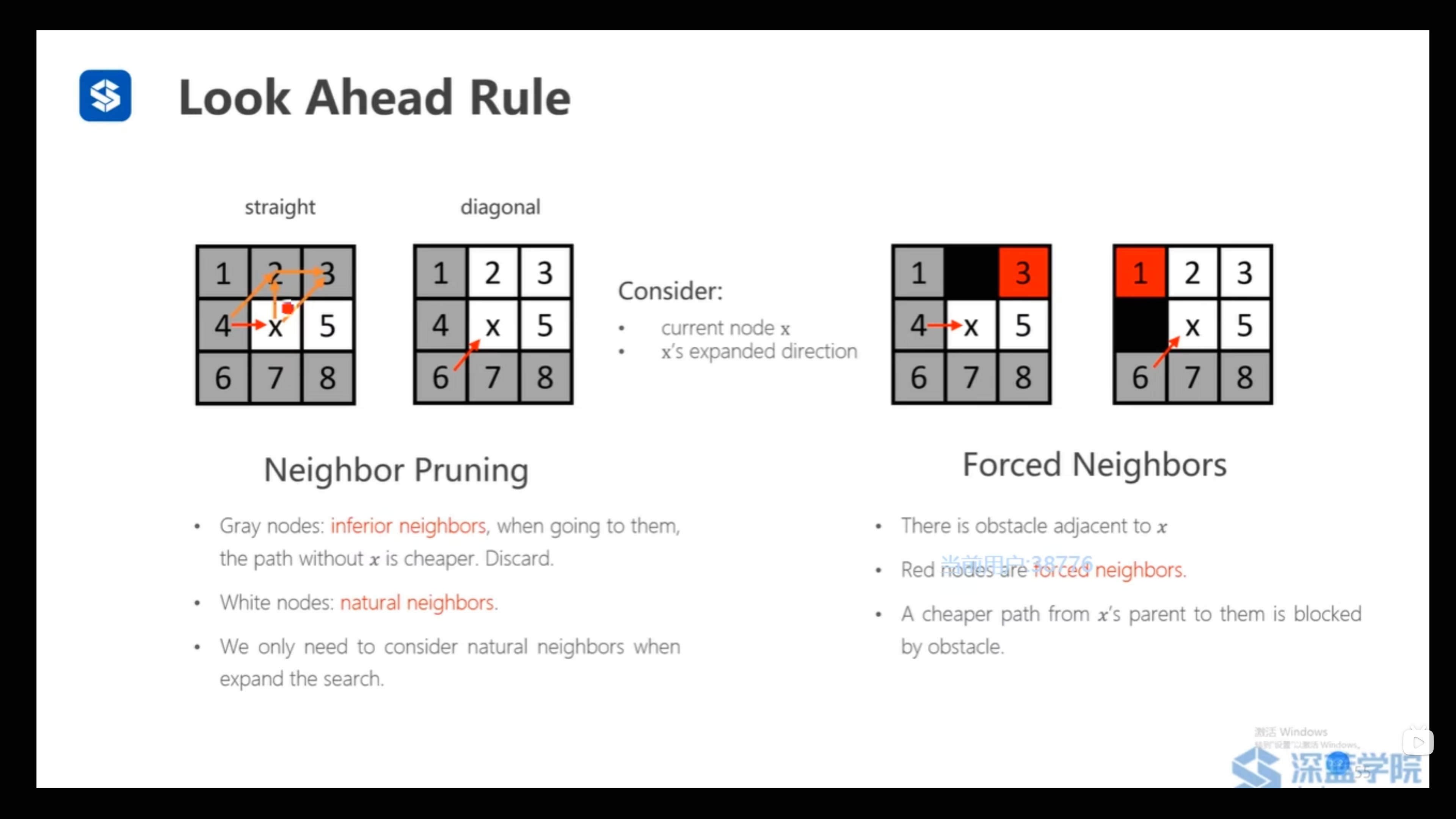
劣性邻居节点:不通过x点的代价更小的点(这种情况下就没有必要通过x点拓展这些劣性邻居节点)(分为x从直线方向拓展和斜线方向拓展的两种情况)
自然邻居节点
强迫邻居节点:原来代价更小的情况被障碍物挡住(两种情况)
需要拓展的节点为自然邻居节点和强迫邻居节点。
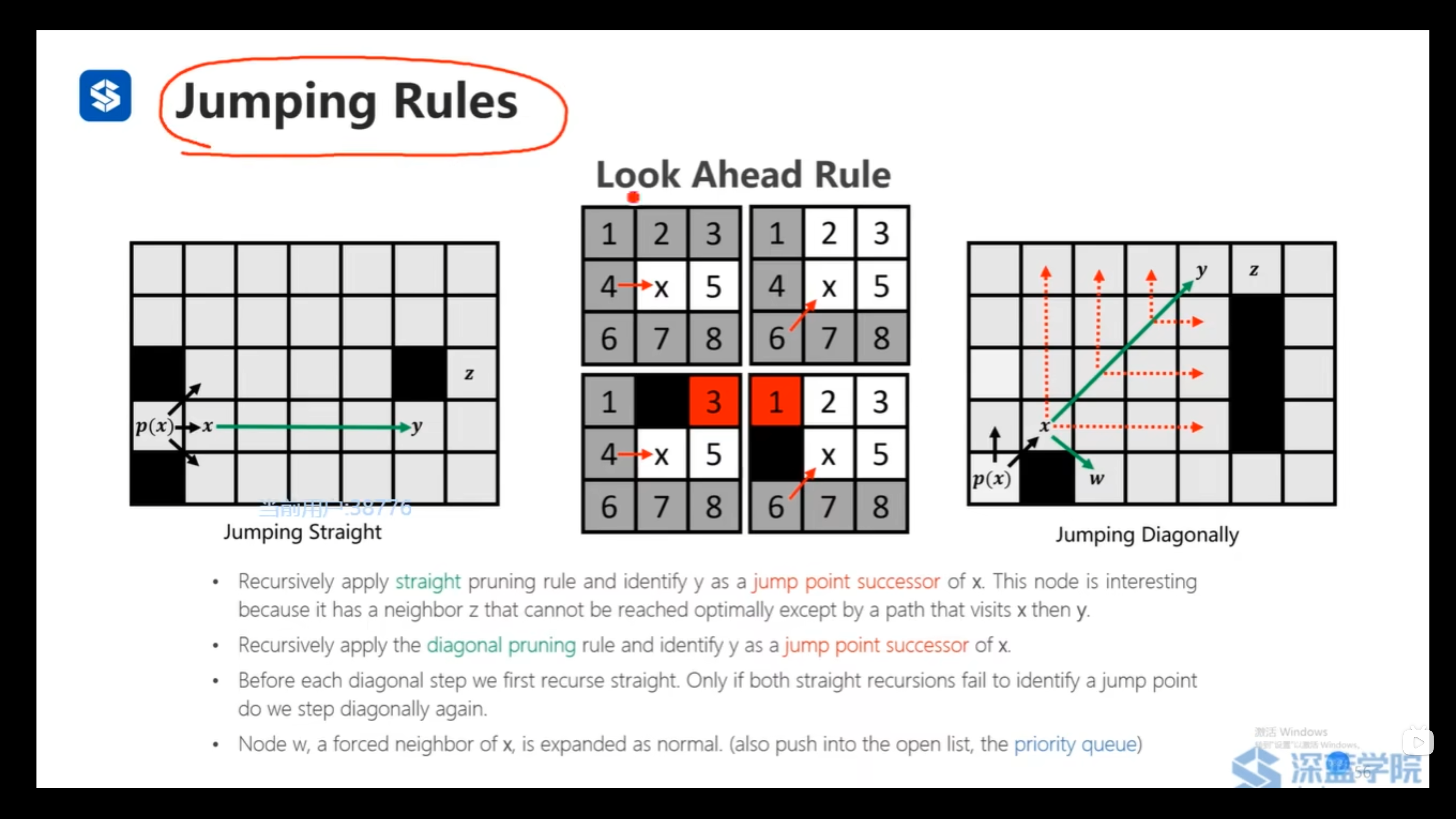
节点x的拓展:
- 应用直线方向的Look Ahead Rule尝试找到后继跳点(后继跳点存在Force Neighbors)
- 应用斜线方向的Look Ahead Rule尝试找到后继jump跳点
- 先拓展直线方向,再拓展斜线方向
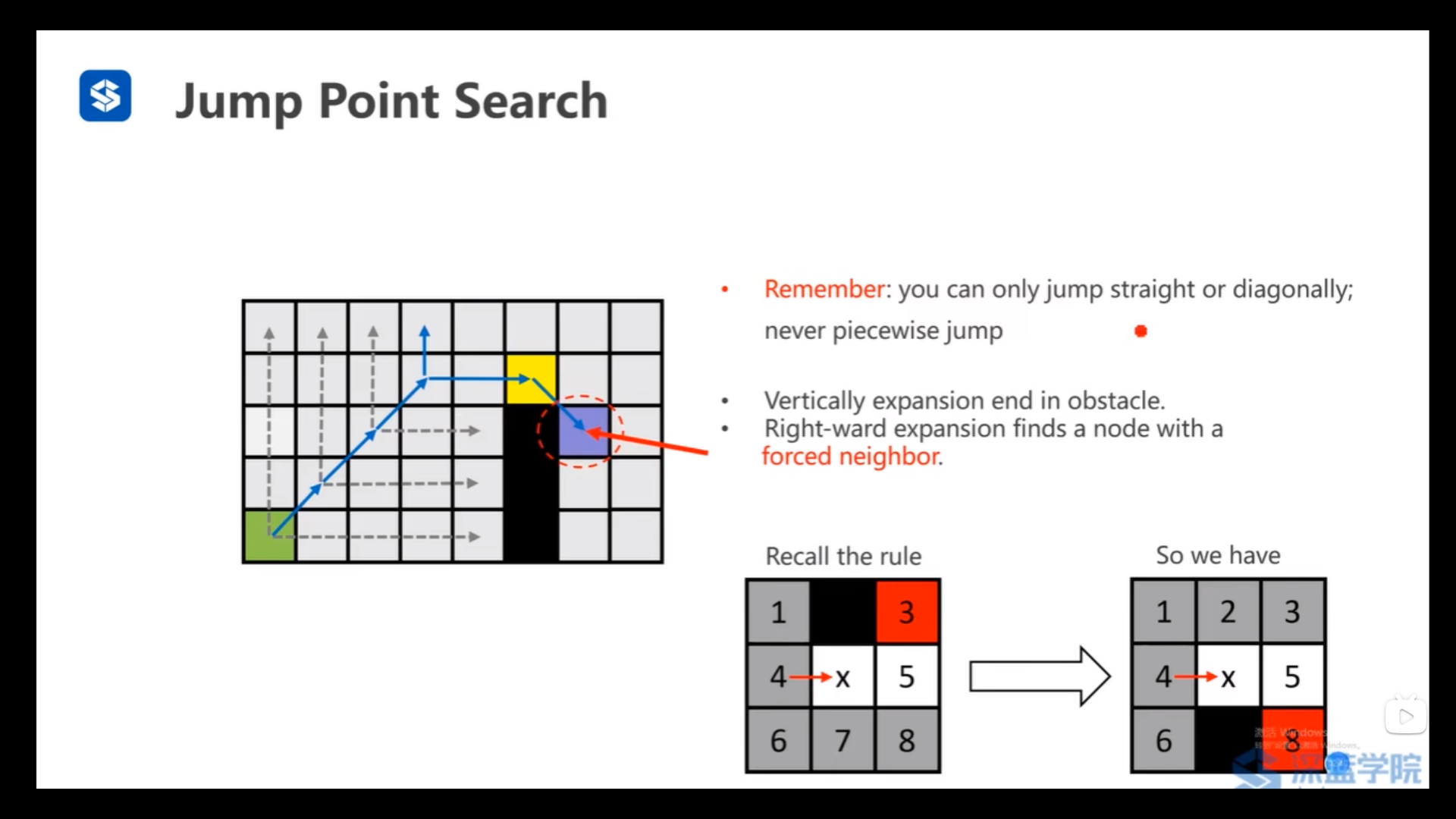
找到的后继跳点要么沿斜线方向要么沿直线方向(例如,不能直接从绿色点跳到黄色点)jump
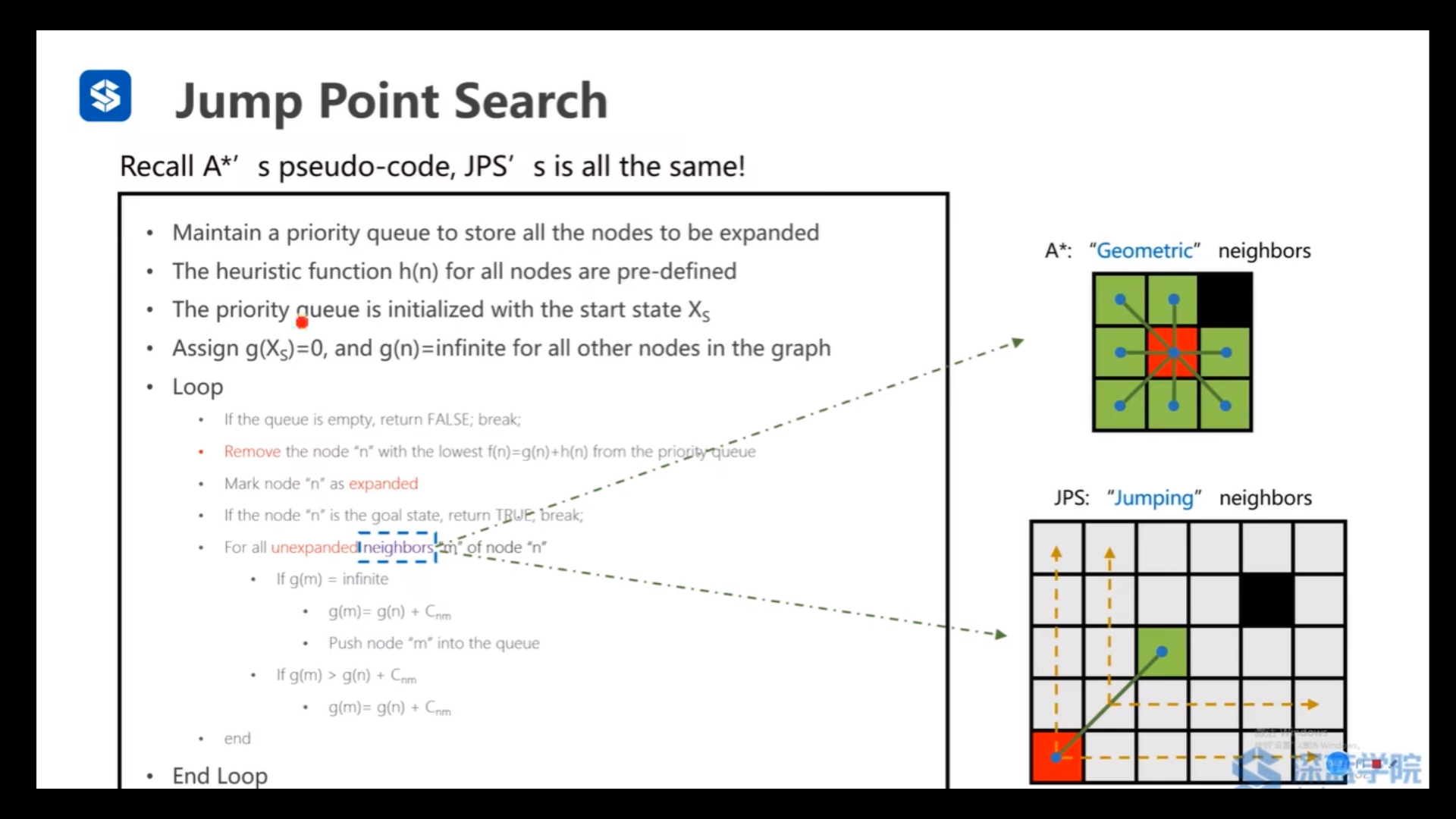
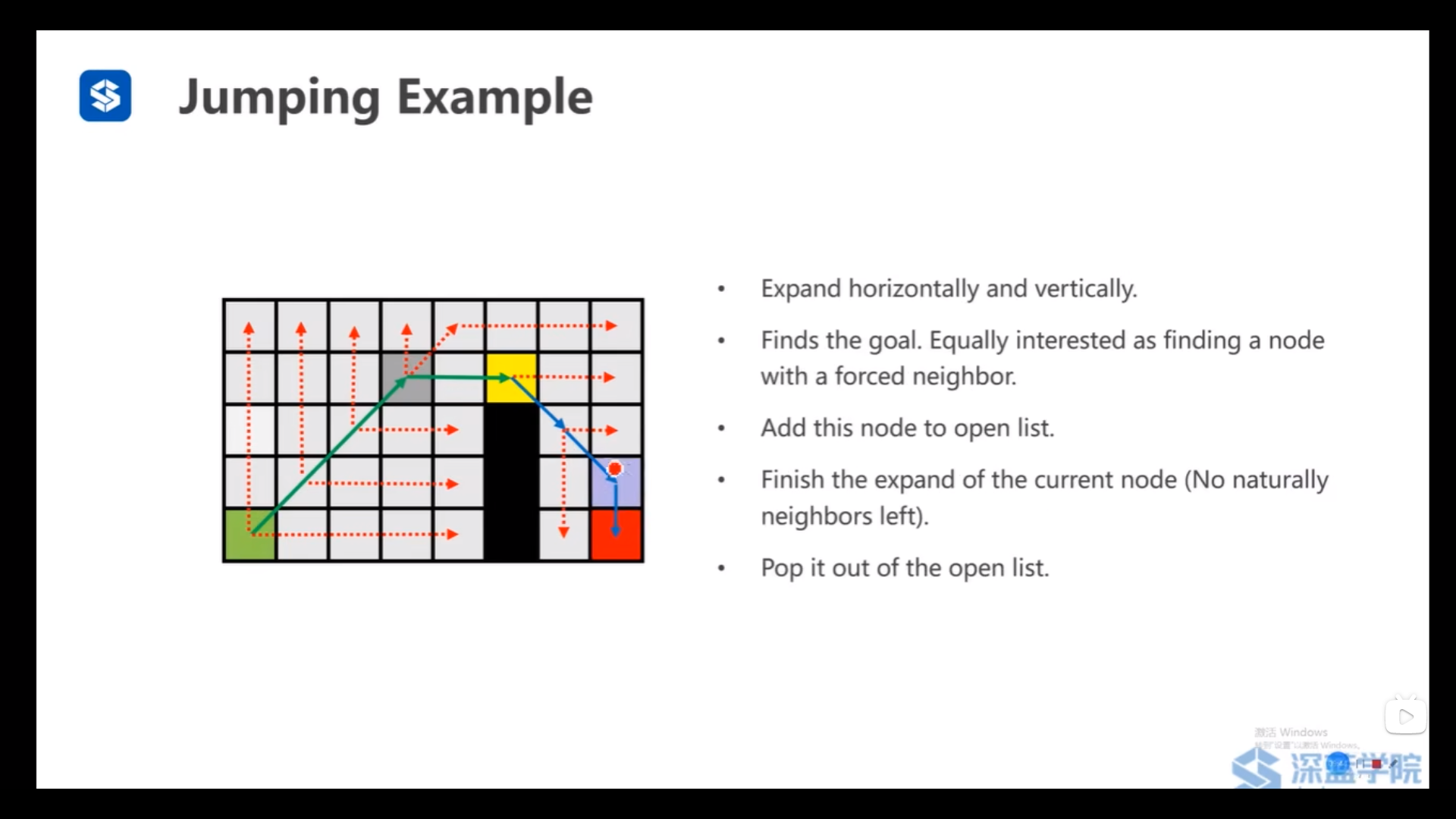
JPS的拓展邻居的方法——沿个各个方向找跳点,当某个方向找到跳点或者到底后就停止本方向本轮的搜索
JPS3D

-
JPS一般来说使用于障碍物较多、环境较为复杂的场合,在障碍物较少的情况下性能会劣于
A*(JPS减少了添加到openlist节点里的个数,但是增加了访问的节点数)
-
JPS只适用于栅格地图
